Math Poetry
(Note from many years later)
For whatever reason, when I first started 3blue1brown, I also found myself jotting down silly math poems on the side. Math is often most naturally expressed with symbols or pictures, and words are a more tricky medium, so something about the added constraint of making those words adhere to certain meters or rhyming structures felt like a fun puzzle, albeit an unabashedly cheesy one.
After I made the first couple of 3blue1brown videos, and put together a website with some vague sense that that's what I was supposed to do, I tossed up the poems to that site while I was at it. Even if they seem a bit strange now, I still find a certain charm in leaving them here as a remnant of that early-2015 mindset associated with trying something wacky and throwing it up online, which was the same mindset which led to the channel in the first place.
Moser's Circle Problem
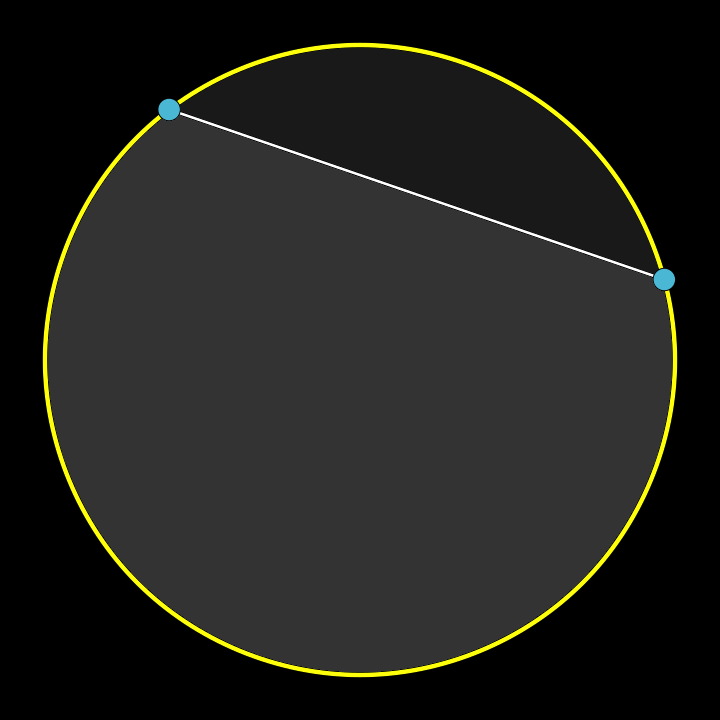
Take two points on a circle,
and draw a line straight through.
The space that was encircled
is divided into two.
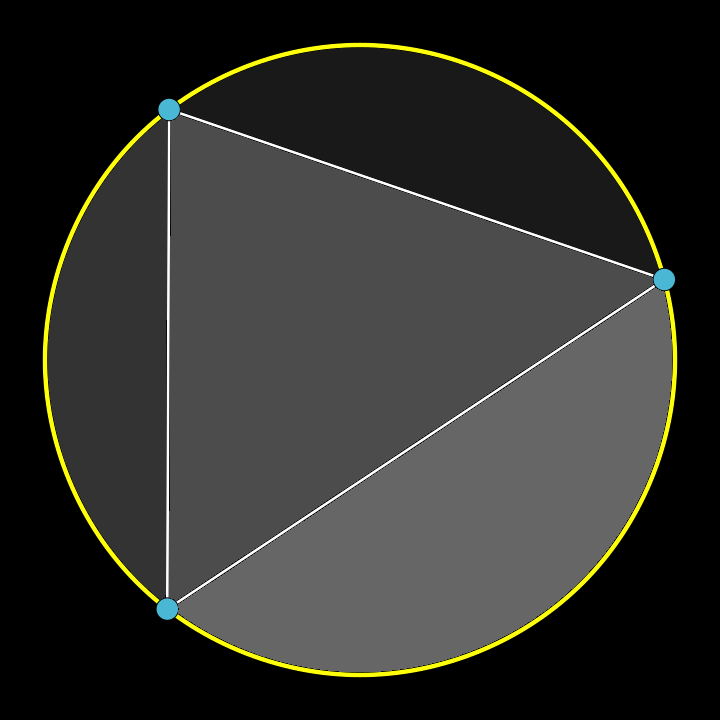
To these points add a third one,
which gives us two more chords.
The space through which these lines run
has been fissured into four.
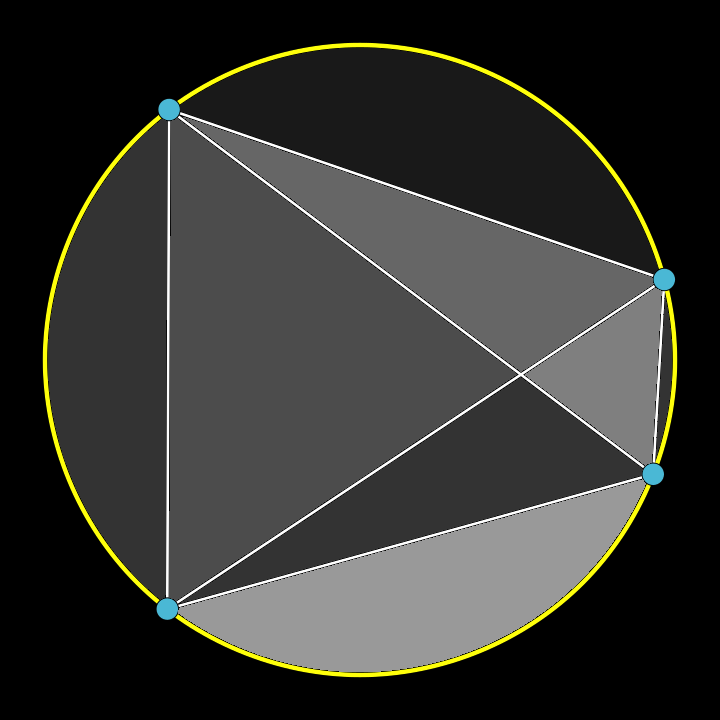
Continue with a fourth point,
and three more lines drawn straight.
The new number of disjoint
regions sums, in all, to eight.
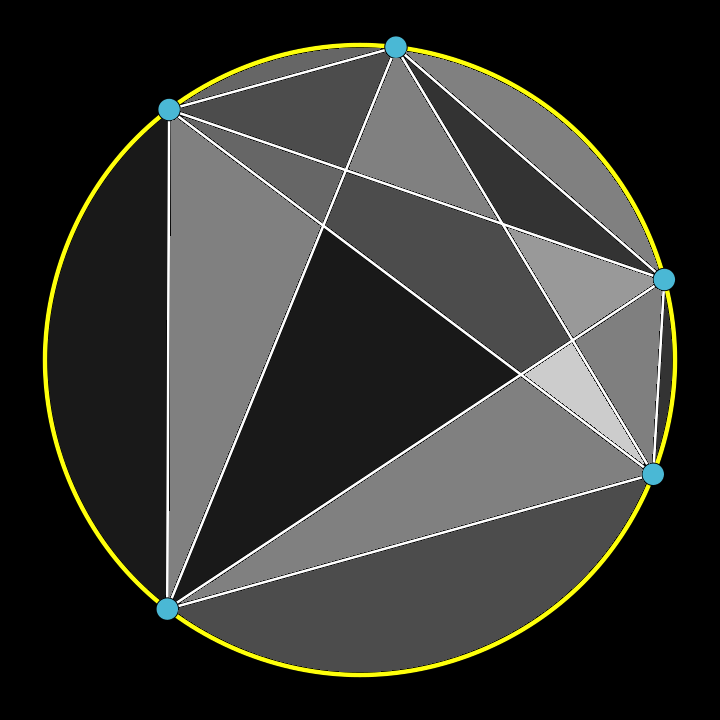
A fifth point and its four lines
support this pattern gleaned.
Counting sections, one divines
that there are now sixteen.
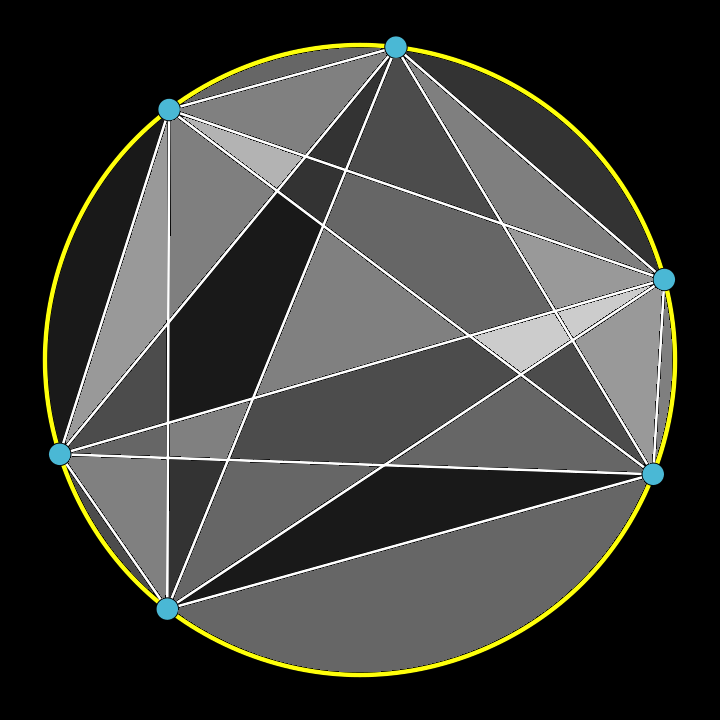
This pattern here of doubling
does seems a sturdy one.
But one more step is troubling
as the sixth gives thirty-one.
Primes
The primes,
through times,
mystified
those who pried.
One fact answers why
they’re simple yet sly:
Layers of abstraction yield
complex forms when pierced and peeled.
Addition lies under multiplication,
defining him as repeated summation.
Then he defines primes as the atoms of integers,
for when multiplied, they give numbers their signatures.
But when we breach the layer between these two distinct operations,
asking about how primes add and subtract, there are endless frustrations.
Even innocuous questions, “what are all their sums?”, or “how often do they differ by two?”,
stump everyone who has ever lived, with progress made only quite recently by just a few.
However, to recruit for and progress math we need to have such questions which can be phrased simply and remain unsolved.
What child does not hear such conjectures and dream, if only for a moment, that they will be the one to see them resolved?
For otherwise the once vigorous curiosity of a child towards math’s patterns, as they grow older, tends to grow tame,
just as the rhyme and rhythm of the primes seems to fade as numbers grow, though in both the underlying patterns remain the same.
All Numbers are Interesting
Is any number that we count banal,
and lacking in a feature one might note?
Suppose some are, and gather up them all.
The smallest one has quite the cause to gloat.
It is precisely how far one must count
before the numbers get uninteresting.
But this would be a curious amount,
which contradicts how we defined the thing!
So every number has something to show,
including ones whom we will never know.
Let’s see if this joke proof applies as well
to real numbers; do they all stand out?
Suppose some don’t, and find one who rebels
by being meaningful beyond a doubt.
Before it was the smallest who amused,
but real sets might lack a minimum.
Will there be a special one to choose
from subsets of the whole continuum?
It isn’t clear where such a choice comes from,
yet some treat “choice” like it’s an axiom.
Invention vs Discovery
A lurking question, old as Greece, does ask:
Is math invention or discovery?
The answer’s both, but here the harder task
is knowing how it switches. So you see,
most truths are found with constructs, which in turn
are built from truths like chickens and their eggs.
One needs to know, should this fact raise concern,
that constructs can be daft; just logic’s dregs.
The truths discovered tell how to define
the structures that make math and world align.
Pythagoras’s theorem about lengths,
is one such truth that he (and others) found.
Observed, discovered, and through mental strength,
it was then proved with pictures that astound.
Much later mathematicians, minds alit,
would formalize, as sets, both “length” and “space”.
These constructs were defined so that by writ
Pythagoras’s truth remains the case.
That is, this “theorem” now seems just defined.
As such, one might then lose their peace of mind.
So in this world where "space" is formalized,
do all those pretty proofs now lose their charm?
Of course not! We all ought to realize
how “length” could change its meaning without harm
to mathematical consistency
in all the theory giving facts of space.
However, then these “facts” would hardly be
related to the nature we embrace.
And hence, a truth has told how to define
a structure that makes math and world align.
2π
Fixed poorly in notation with that two,
you shine so loud that you deserve a name.
Late though we are, to make a change it's true,
We can extol you ‘til you have pi's fame.
One might object, "Conventions matter not!
Great formulae cast truths transcending names."
I've noticed, though, how language molds my thoughts;
the natural terms make heart and head the same.
So lose the two inside your autograph,
then guide our thoughts without you "better" half.
Wonders math imparts become so neat
when phrased with you, and pi remains off-screen.
Sine and exp both cycle to your beat.
Jive with Fourier, and forms are clean.
“Wait! Area of circles”, pi would say,
“sticks oddly to one half when tau’s preferred.”
More to you then! For write it in this way,
then links to triangles can be inferred.
Nix pi, then all within geometry
shines clean and clear, as if by poetry.
1-1+1-1+...
When one takes one from one
plus one from one plus one
and on and on but ends
anon then starts again,
then some sums sum to one,
to zero other ones.
One wonders who'd have won
had stopping not been done;
had he summed every bit
until the infinite.
Lest you should think that such
less well-known sums are much
ado about nonsense
I do give these two cents:
The universe has got
an answer which is not
what most would first surmise,
it is a compromise,
and though it seems a laugh
the universe gives “half”.
Defining Math
In math, we strive and stickle with a pride,
to wash away all ambiguity.
And yet, definers cannot all decide
what “math” itself means. What an irony!
Perhaps a science, solving mysteries,
but happy to pursue what seems absurd.
Perhaps a brother of philosophies,
but with a rigid rigour in each word.
Computer science might be suitable,
but most of math is not computable.
Perhaps it is a language of its own,
which, as to english, has the most false friends.
Perhaps religion, where the truth alone
is worshiped, giving means as well as ends.
Perhaps a sister of creative arts,
but one arousing reason, not a sense.
Indeed it shares a number of its parts
with almost every study in some sense.
But it’s an orphan, floating in abstract,
and it alone encloses what’s exact
Euler's Formula
Famously
start with e,
raise to π
with an i.
we've been taught
by a lot
that you've got
minus one.
Can we glean
what it means?
For such words
are absurd.
How to treat
the repeat
of a feat
πi times?
This is bound
to confound
'til your mind
redefines
these amounts
one can't count
which surmount
our friend e.
Numbers act
as abstract
functions which
slide the rich
2d space
in its place
with a grace
when they sum.
Multiplied,
they don’t slide,
acting a
second way.
They rotate,
and dilate,
but keep straight
that same plane.
Now what we
write as e
to the x
won’t perplex
when you know
it’s for show
that “x" goes
up and right.
It does not,
as you thought,
repeat e
product e.
It functions
with gumption
on functions
of the plane.
It turns slides
side to side
into growths
and shrinks both.
Up and downs
come around
as turns round,
which is key!
This is why
π times i,
which slides north
is brought forth
and returned,
we have learned,
as a turn
halfway round.
Minus one,
matched by none,
turns this way,
hence we’re done.
Ode To Infinity
Philosophers have claimed you are not "real",
but you are no less true than 3, in fact.
For what is "three"? Some thinking will reveal,
a term that points to triplets in abstract.
And so are you, a pointer in this light,
but aimed instead at families without size.
From here it took great Cantor's mental sight
to see these sets disjoin before his eyes.
For that's the tricky thing about you, friend,
what you are is something without end!
Aside from all the masks you wear as sets,
you permeate all math like pi and e.
Without you series, sequences and nets,
would vanish, as would all geometry.
To cook the real numbers all it takes,
is you and all the fractions to react.
When added as a simple point you make
both arguments and spaces more compact.
When patterns, lists and odes drag on and on,
just say "infinity", and woes are gone.
Groups
"What is a group?"
“A symmetry of things.”
“Of things from where?”
“Oh, those from any place.”
“But where in math?”
“In math? A vector space.”
“And what is that?”
“It’s what a field brings.”
“And what are fields?”
“They’re Symmetries of groups.”
“A group’s own group?”
“Why yes, when both are one.”
“So now we’re back?”
“Indeed, where we’d begun.”
“So where to start?”
“Where you start any loop.”
“And where is that?”
“From anywhere within.”
“And if you're out?”
“Then why would you begin?”
Abstraction
The crux of thought,
computer science,
language, and how math arose,
abstraction brought
a key alliance
syncing facts who seem opposed.
The first is how
our minds are tuned to
focus on at most one thought.
Though well endowed,
they’re not immune to
puzzlement when overwrought.
But secondly
the facts of nature
interweave dependently,
so how do we
conceive this nature
in its multiplicity?
We first extract
a common trait
of things too complex to be known,
then to “abstract”,
reformulate
this trait as something in its own.
As such it’s pulled
from all distractions,
single, hence conceivable.
But when minds hold
this dense abstraction,
They enclose a system whole.
For “things” and their “traits”,
though separately named,
do more than relate:
They’re one and the same.