Group theory, abstraction, and the 196,883-dimensional monster
An introduction to symmetry, group theory, isomorphisms, and the monster group.
This project is part of the MegaFavNumbers collaboration, many members of the YouTube math community are making videos about their favorite numbers over 1,000,000.
My Favorite Mega Number
The number we'll be looking at is considerably larger than one million, roughly 8\times10^{53}.
\color{purple}808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000\\=2^{46}\cdot 3^{20}\cdot 5^9\cdot 7^6\cdot 11^2\cdot13^3\cdot 17\cdot 19\cdot 23\cdot 29\cdot 31\cdot 41\cdot 47\cdot 59\cdot 71
To give a sense of scale, it's around the number of atoms in Jupiter. It might seem completely arbitrary, but I love that if you were to talk with an alien civilization or a super-intelligent AI that invented math for itself without any connection to our particular culture or experience, I think both would agree this number is quite peculiar and reflects something fundamental.
What is this number, exactly? Well, it's the size of the monster, but to explain that we'll need to back up and talk about group theory.
Interesting!
Intuitive Definition of a Group
This field of study is all about codifying the idea of symmetry. For example, when we say a face is symmetric, we mean you can reflect it about a line, and it's left looking completely the same; it's a statement about an action you can take.
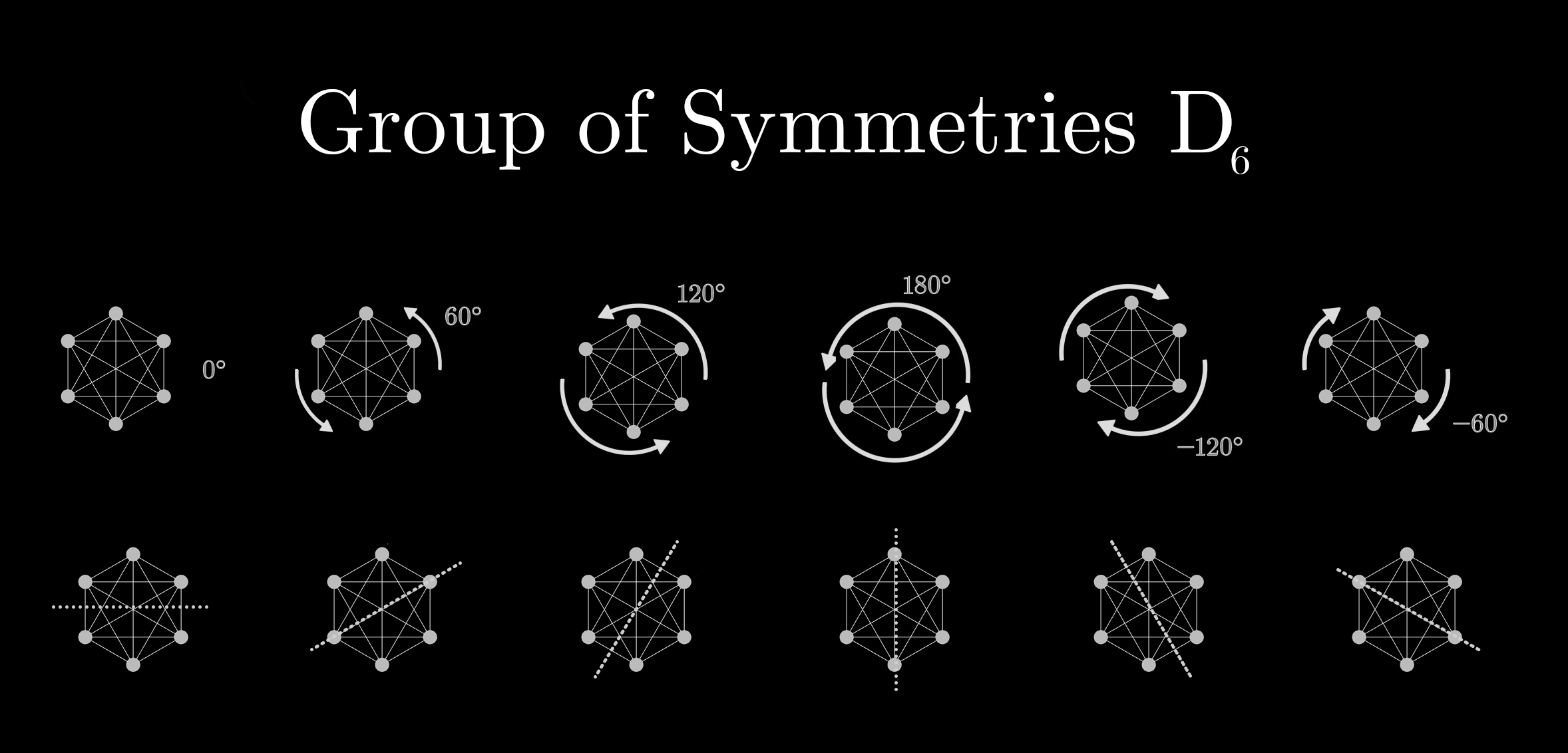
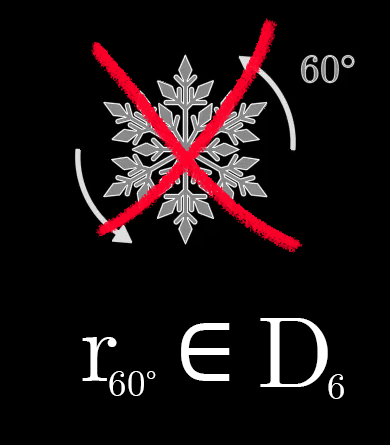
Something like a snowflake is symmetric in more ways. You can rotate it 60 degrees, or 120 degrees, or flip it along various different axes, and all these actions still leave it looking the same.
A collection of all actions like this taken together is called a "group." Well… kind of, groups are typically defined more abstractly than this, but we'll get to that later. The fact that mathematicians have opted to use such an otherwise generic word for this seemingly specific kind of collection gives you some sense how fundamental they find it.
We always consider the action of doing nothing to be part of a group, so including this do-nothing action, the group of symmetries of a snowflake includes 12 distinct actions. It even has a fancy name, D_6.
The simple group of symmetries with only two elements acting on a face also has a fancy name, C_2. In general, there's a whole zoo of groups, with no shortage of jargon in their names, categorizing all the different ways that something can be symmetric.
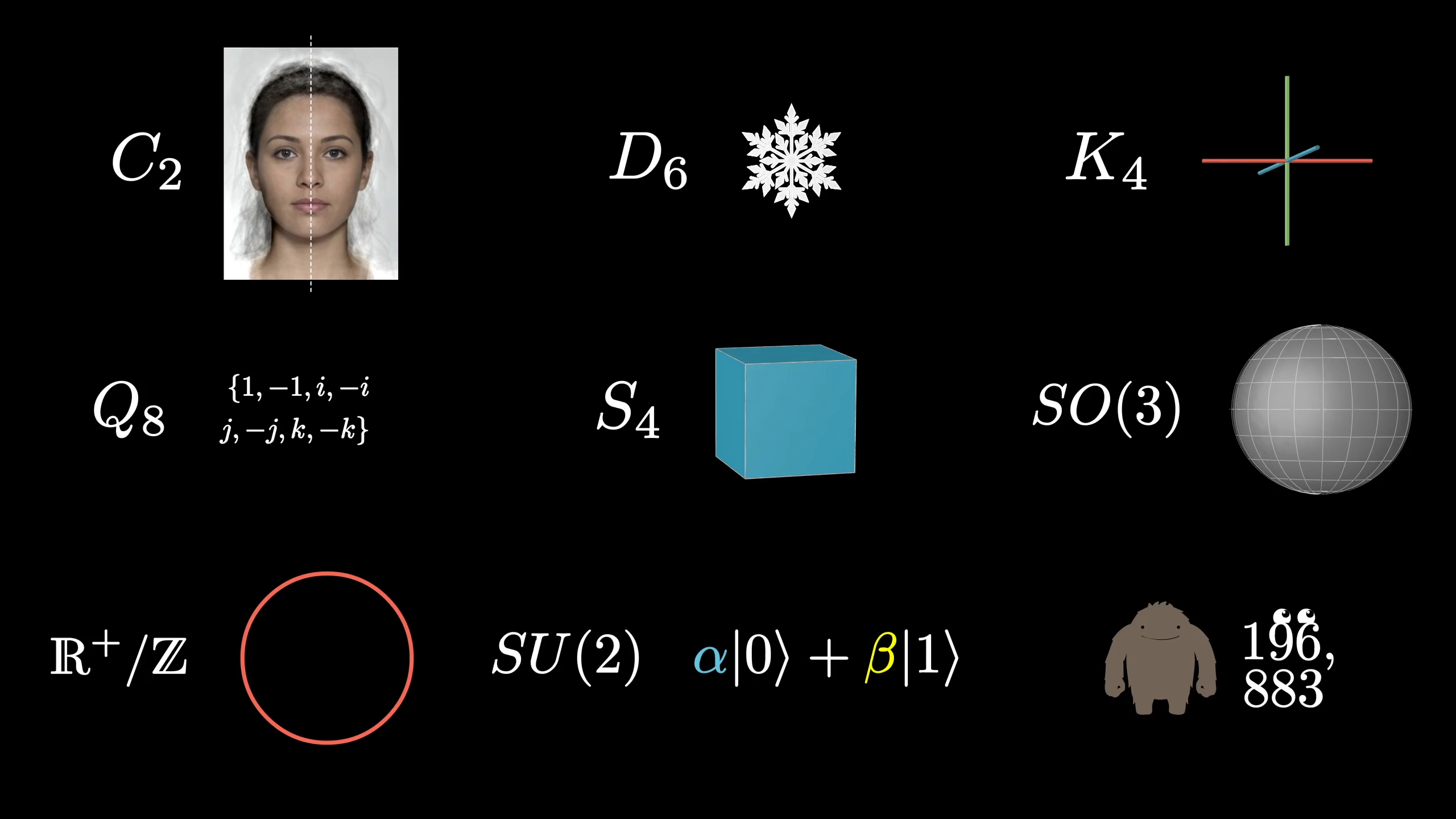
When we describe these sorts of actions, there's always some implicit structure in the object that we're preserving. For example, there are 24 rotations I can apply to a cube that leave it looking the same, and those 24 actions do indeed constitute a group.
But if we allow reflections, which is kind of a way of saying the orientation of the cube is not part of its structure that we're preserving, there are 48 actions in total; a larger group.
If we consider the faces to be a little less rigidly attached, free to rotate and get shuffled around, you get a much larger set of actions. All these shuffling rotating actions on the set of faces also forms a group. It's a much more complicated group, but a valid group nonetheless. The large size of this group reflects the much looser sense of structure that each action preserves.
Each face of the cube is free to switch places and rotate or flip along the
way. This creates a group with (8^6)(6!) symmetries.
The loosest sense of structure is if we have a collection of points and consider any way to shuffle them, any permutation, to be a symmetry of these points. Unconstrained by any underlying property to be preserved, these permutation groups can get quite large.
In total, there are 6!=720 actions in this permutation group. By contrast, if we take these points to be corners of a hexagon and only consider permutations which preserve how far apart they all are from each other, we get only the 12 snowflake symmetries we saw earlier.
Bump the number of points up to 12, and the number of permutations grows to about 479 million. The monster that we'll get to is rather large, but it's important to understand that largeness in and of itself isn't all that interesting with groups; the permutation groups already make that easy to see. The group of permutations for 101 objects with its 101 factorial different actions has a size of 101!\approx 9.43\times10^{159}. If every atom in the observable universe had a copy of our universe inside it, this is roughly how many sub-atoms there would be.
These permutation groups go by the name S_n, and they play an important role in group theory. In a certain sense, they encompass all other groups. So far this might all seem intellectually playful, but you might wonder if any of this is actually useful.
One of the earliest applications of group theory came when mathematicians realized that the structure of these permutation groups tells us something about solutions to polynomial equations. You know how in order to find the two roots of a quadratic equation, everyone learns a certain formula in school? Lesser known is the fact that there's also a cubic formula, which involves nesting cube roots with square roots. There's even a quartic formula for degree 4 polynomials, though it's an absolute mess. For the longest time mathematicians struggled to find a formula to solve degree 5 polynomials.
\begin{align*}
\text{Quadratic formula }&\quad\frac{-b\pm\sqrt{b^2-4ac}}{2a} \\
\text{Cubic formula }&\quad\sqrt[3]{-\frac q2+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}+\sqrt[3]{-\frac q2-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}} \\
\text{Quartic formula }&\quad r_i=-\frac{b}{4a}-S\pm\frac12\sqrt{-4S^2-2p\pm\frac qS} \text{ where...}\\
\text{Quintic formula }&\quad ???
\end{align*}It turns out that if you think about the group which permutes the roots of such a polynomial, there's something about the nature of this group that reveals that no quintic formula can exist. For example, the 5 roots of the polynomial seen below have definite values, but you can never write down those exact values by starting with the coefficients and using the four basic operations of arithmetic and radicals, analogous to the quadratic formula. And that impossibility has everything to do with the inner structure of the permutation group S_5.
A theme in math through the last two centuries has been that the nature of symmetry in and of itself can show us all sorts of non-obvious facts about the other objects we study.
To give just a hint of one of the many ways this applies to physics, there's a beautiful fact known as Noether's theorem saying that every conservation law corresponds to some kind of symmetry, a certain group. So all these fundamental laws like conservation of momentum and energy each correspond to a certain group.
\text{Noether's Theorem} \\\ \\
\begin{aligned}
\color{blue}\text{Conservation law}\color{black}&\Leftrightarrow \color{green}\text{Symmetry} \\
\color{blue}\text{Momentum}\color{black}&\Leftrightarrow \color{green}\text{Translation in space} \\
\color{blue}\text{Energy}\color{black}&\Leftrightarrow \color{green}\text{Translation in time}
\end{aligned}All of this is to say that groups really are fundamental, and the one thing I want you to recognize right now is that they're one of the most natural things you could study. What could be more universal than symmetry? So you might think the patterns among groups themselves would somehow be very beautiful and symmetric. The monster, however, tells a different story.
Before we get to the monster, at this point some mathematicians might complain that what I've described so far are not groups, but group actions. They might argue that groups are something slightly more abstract.
By way of analogy, if I mention the number "3", you probably don't think about any specific triplet of things. You probably think 3 as an object in and of itself, an abstraction, represented with a common symbol.
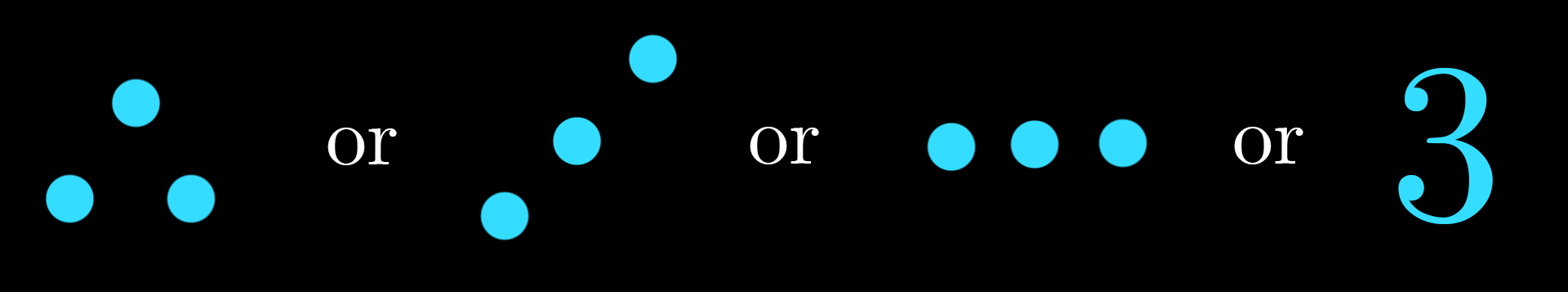
In much the same way, when mathematicians discuss the elements of a group, they don't necessarily think about specific actions on a specific object, they might think of these elements as things in and of themselves, maybe represented with symbols.
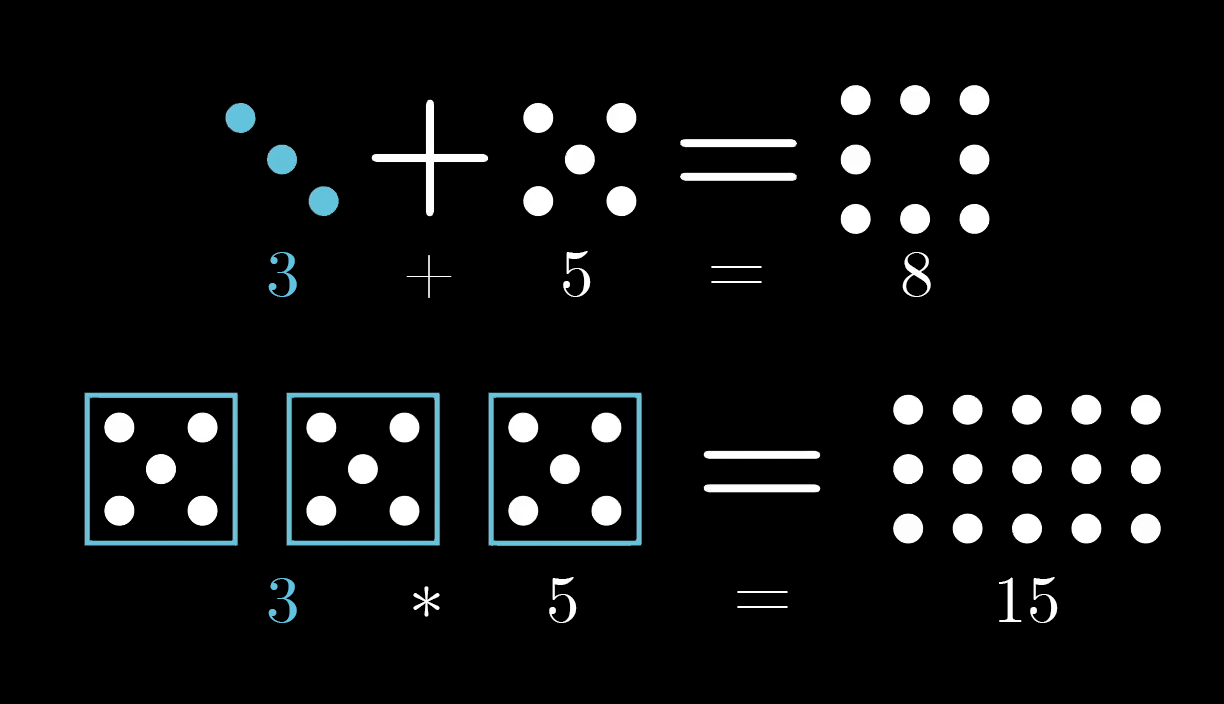
For something like the number three, the abstract symbol does very little good unless we define its relation with other numbers, for example the way it adds and multiplies with them. For each of these, you could think of a literal triplet of something, but again most of us are comfortable, probably more comfortable, using the symbol alone.
Similarly, what defines a group are all the ways its elements combine with each other. In terms of actions, what we mean by combining is to apply one after the other, read from right to left; if you flip a snowflake about the x-axis, then rotate it 60 degrees counterclockwise, the overall action is the same as if you had flipped it about this diagonal line.
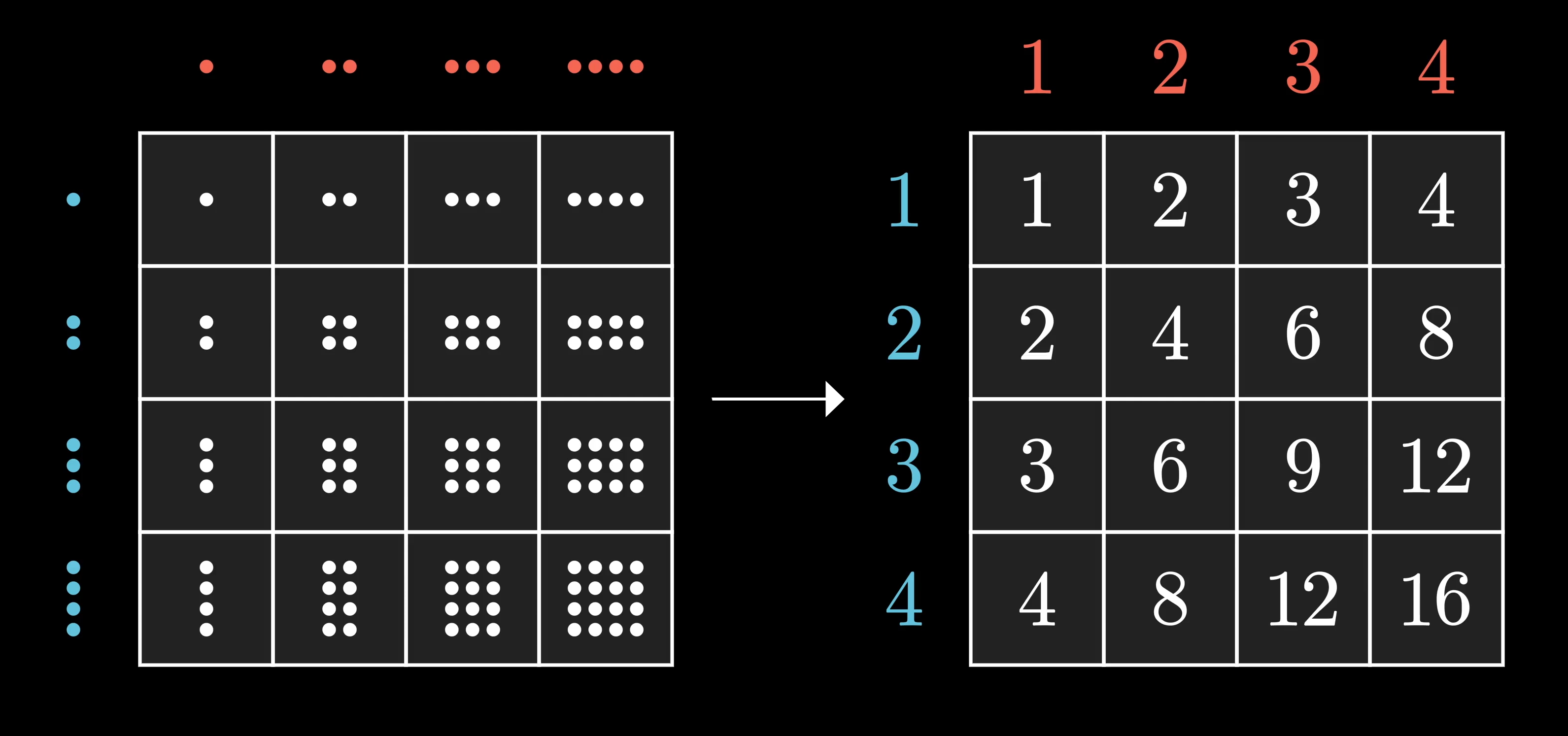
All possible ways to combine two elements like this defines a kind of multiplication in a group. This is what gives a group its structure. We can see the full 8x8 multiplication table for symmetries of a square. If you apply an action on the top row followed by an action on the left column, it's the same as the action in the corresponding grid square.
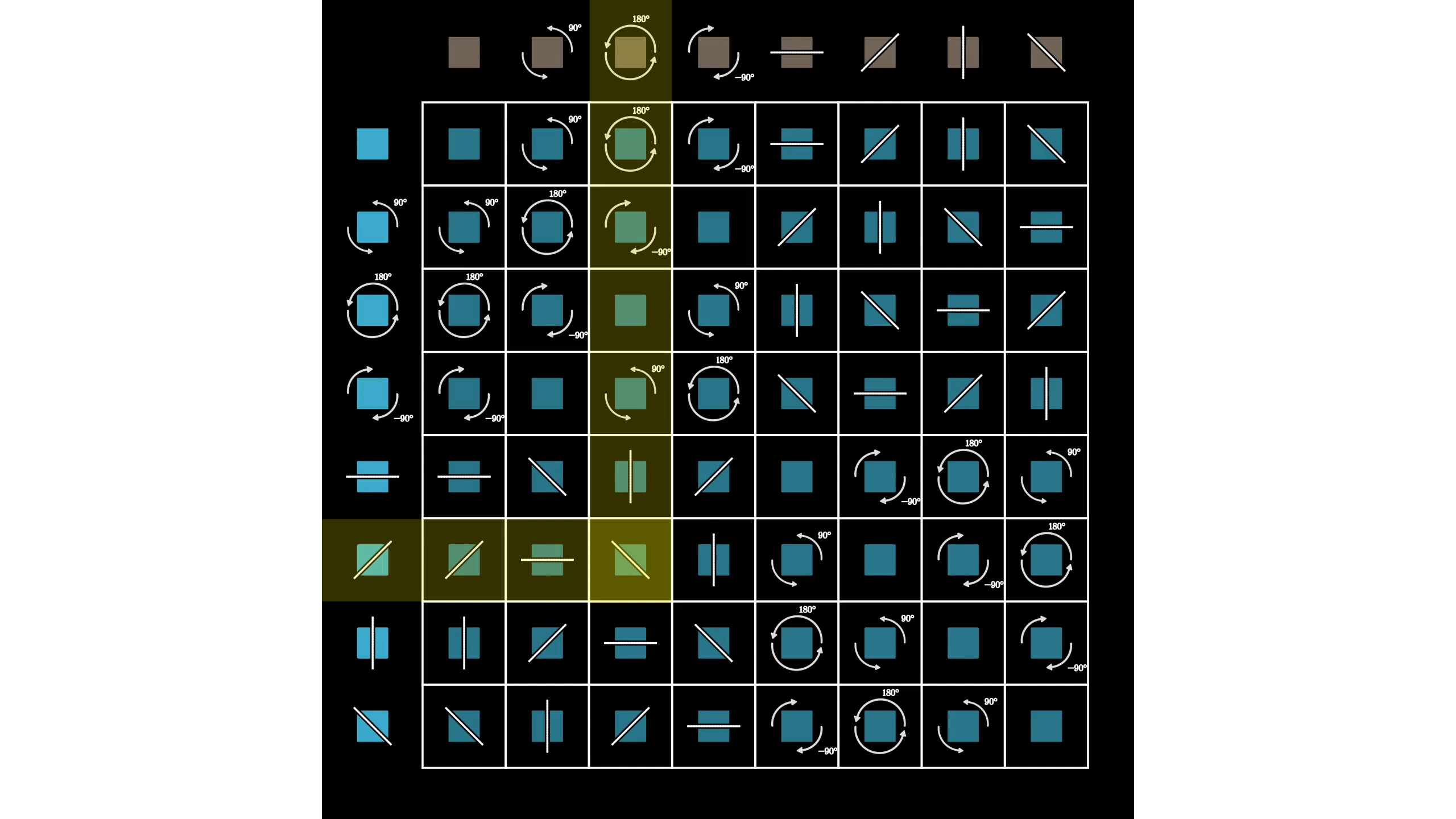
If we replace each of these symmetric actions with something symbolic, the multiplication table still captures the structure of the group, but now it's abstracted away from any specific object it might act on, like a square, or roots of a polynomial.
We can describe the symmetries of a square using symbols for rotation and
reflection across the x axis. Rotating and then reflecting is denoted sr
because actions are read from right to left.
This is entirely analogous to how the usual multiplication table is written symbolically, which abstracts away from the idea of literal counts. Literal counts arguably make it clearer what's going on, but since grade school we all grow comfortable with the symbols. After all, they're less cumbersome, freeing us up to think about more complicated numbers, and also to think about numbers in new and different ways.
All of this is true of groups, which are abstractions above the idea of symmetry actions we've been looking at. I'm emphasizing this for two reasons, one is that understanding what groups really are gives a better appreciation of the monster. The other is that many students learning about groups for the first time can find them frustratingly opaque, I know I did.
Mathematical Definition of a Group
Using cubes and snowflakes provides a useful intuition for what an example of a group is, but how would a mathematician go about describing a group? Specifically, we know that not everything is allowed to be classified as a group, so how do we determine if something is a group or not?
We begin with a set of objects. A set is any collection of things. This could be the set of integers, a set of permutations of n points, or a set of symmetric actions on a geometric shape. When studying groups, we care about how the objects in this set interact with each other. So there must be some notion of combining, or multiplying, two elements.
a\circ b =cHere we have some binary operator \circ. It is called a binary operator because it produces something when it operates on two elements, a and b. It may be helpful to think of a binary operator as a function which works on two inputs: \circ (a,b)=c. What operation this \circ actually performs depends on the group we're looking at.
There are four special rules, called the axioms of groups, that arise from considering what must be true when thinking about composing actions. The first is called the closure axiom which states that the element which results from combining two elements must also be part of the group. Try to think of two symmetric rotations of the snowflake which when applied one after the other produce a rotation that isn't symmetric!
Every action that is composed of symmetric actions is itself symmetric.
The next law is the associative axiom. It states that the order of operator evaluation does not matter. For example, if we wanted to rotate our snowflake 180 degrees, that is the same as rotating by 60 degrees three times. However, our operation is binary, so it can only operate on 2 elements at a time. This axiom means that it doesn't matter if we begin by combining the first two and then merge with the third or if we begin by combining the last two and then merge with the first.
(r_{60^\circ}\circ r_{60^\circ})\circ r_{60^\circ} = r_{60^\circ}\circ (r_{60^\circ}\circ r_{60^\circ})= r_{180^\circ}The third rule is the identity axiom. The identity element is the action of doing nothing, and a group isn't complete without it. Rotating by 180 degrees twice is an identity action, and from the closure axiom we know that the result of two sequential actions must also be part of the group.
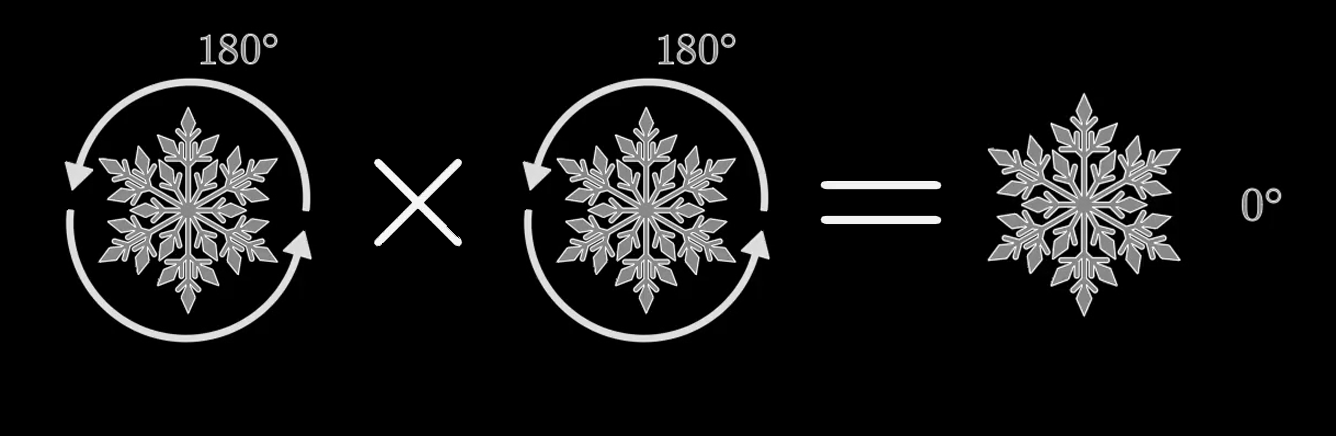
The final condition is the inverse axiom which states that every element of the group also has an inverse element which when multiplied together produce the identity. Rotating 60 degrees clockwise and then 60 degrees counterclockwise is the same as having done nothing, so these two are inverses of each other. Some elements are their own inverse, like reflecting over an axis.
A typical course starts with this formal, abstract definition of a group which can be hard to grasp. A key concept here is that groups are a tool used to describe not just one symmetric object, but all symmetric objects. Similar to how 3 is an example of what a number is, the snowflake is just an example of what a group is. Mathematicians use abstract concepts like numbers and groups because patterns become more obvious and it strengthens connections between different objects. To any students with a future in group theory, I would say if you appreciate this relationship it can help to keep a lot of the course more grounded.
Comparing Different Groups
Previously, we described both the symmetries of a snowflake and the symmetries of a hexagon to be the group D_6. Every action which preserves the structure of a snowflake will also preserve the structure of a hexagon.
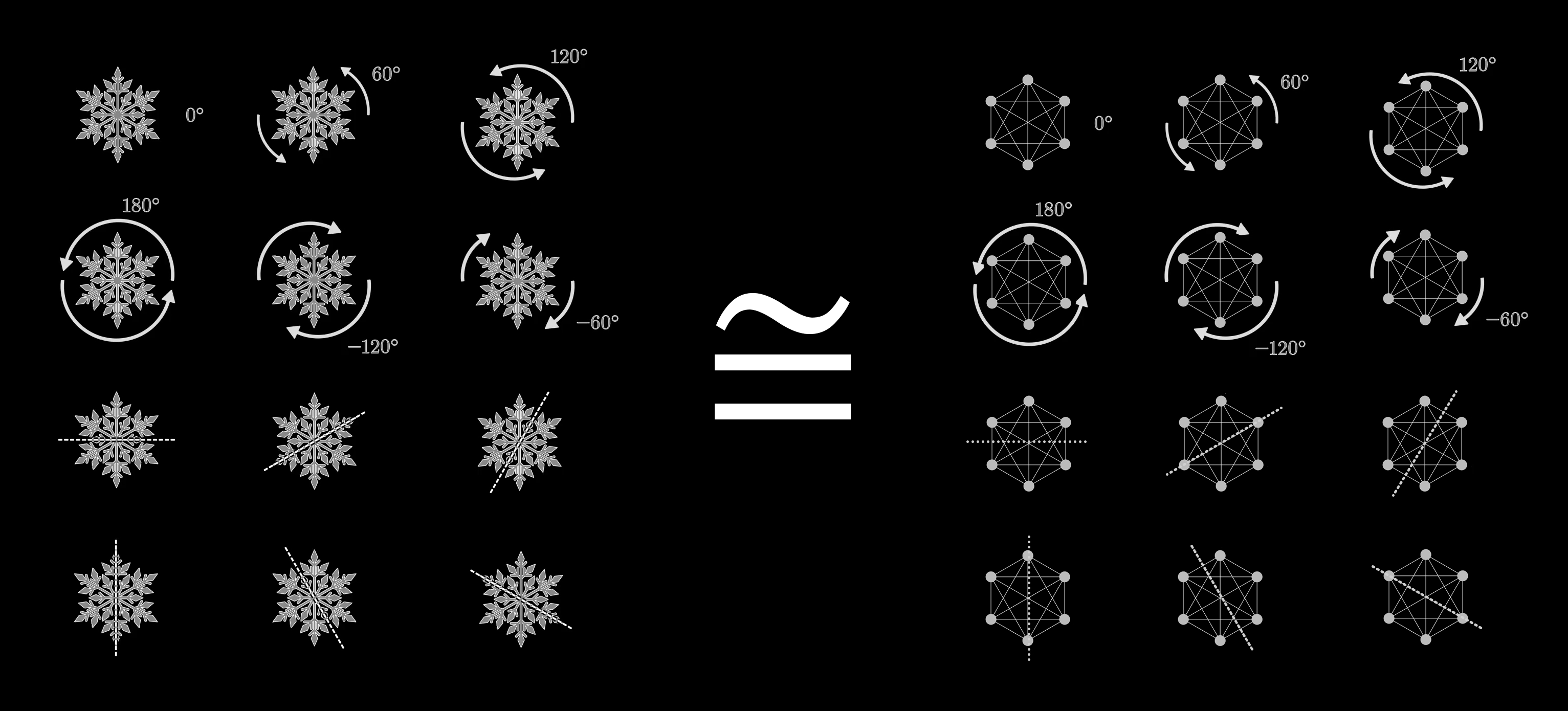
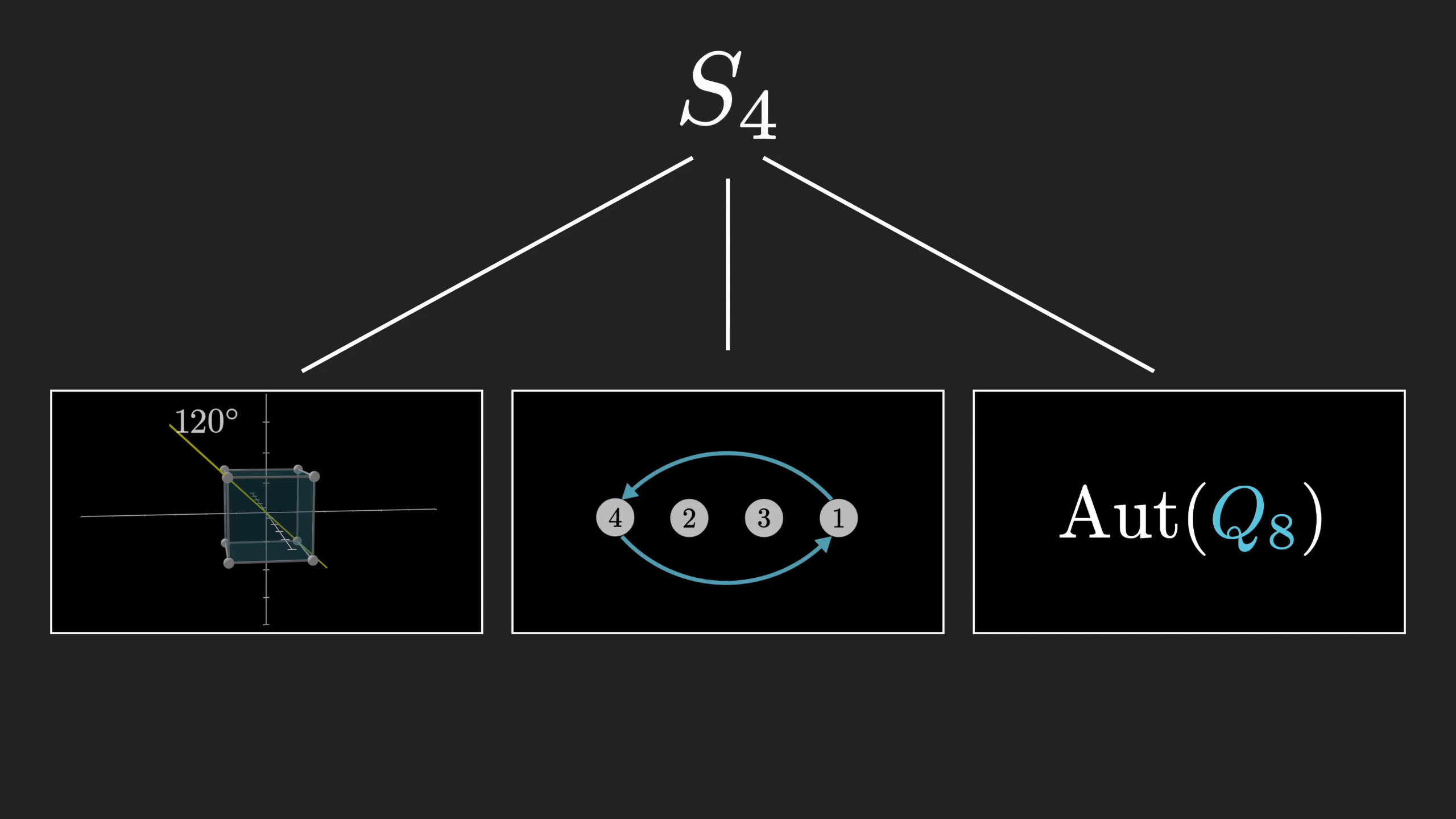
That might seem obvious, a snowflake is basically just a hexagon with a fancy pattern. But a less obvious example might highlight why this kind of abstraction is desirable. Consider the symmetries of a cube and the permutation group of 4 objects. At first, these groups feel very different.
You might think of the cube symmetries as acting on the 8 corners in a way that preserves the distance and orientation structure among them, whereas on the right here we have completely unconstrained actions on a smaller set of four points.
As it happens, though, these two groups are really the same, in the sense that their multiplication tables will look identical. Anything you can say about one group will be true of the other. For example, there are 8 distinct permutations where applying it three times in a row gets you back to where you started (not counting the identity). These are the ones cycling three elements. There are also 8 rotations of a cube that have this property, the 120 & 240 degree rotations about each diagonal. This is no coincidence.
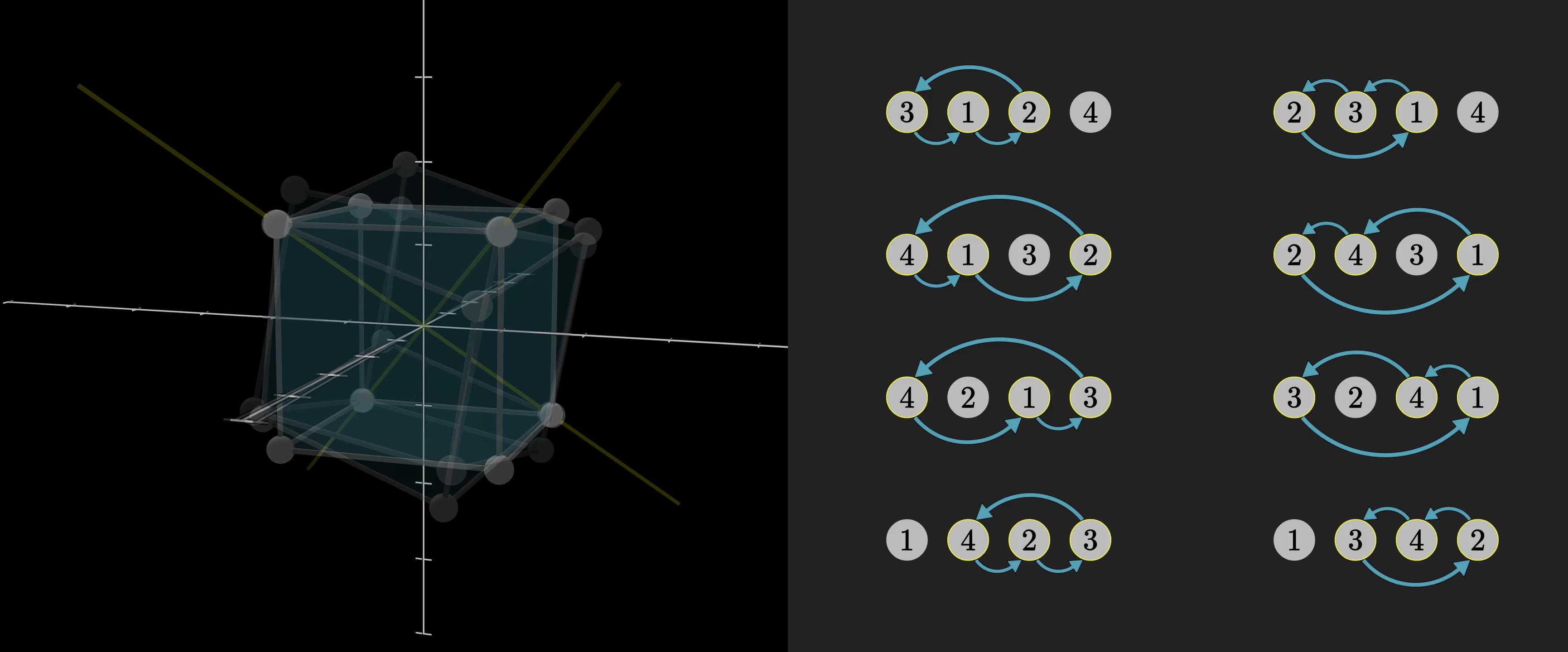
The way to phrase this precisely is to say there's a one-to-one mapping between rotations of a cube and permutation of four elements which preserves composition. For example, if you rotate 180 degrees about the y axis, then 180 about the x axis, the overall effect is the same as a 180 degree rotation about the z-axis. Remember that's what we mean by a product of two actions. If you look at the corresponding permutations, this product is still true, applying the two on the left gives the same effect as applying the one on the right.
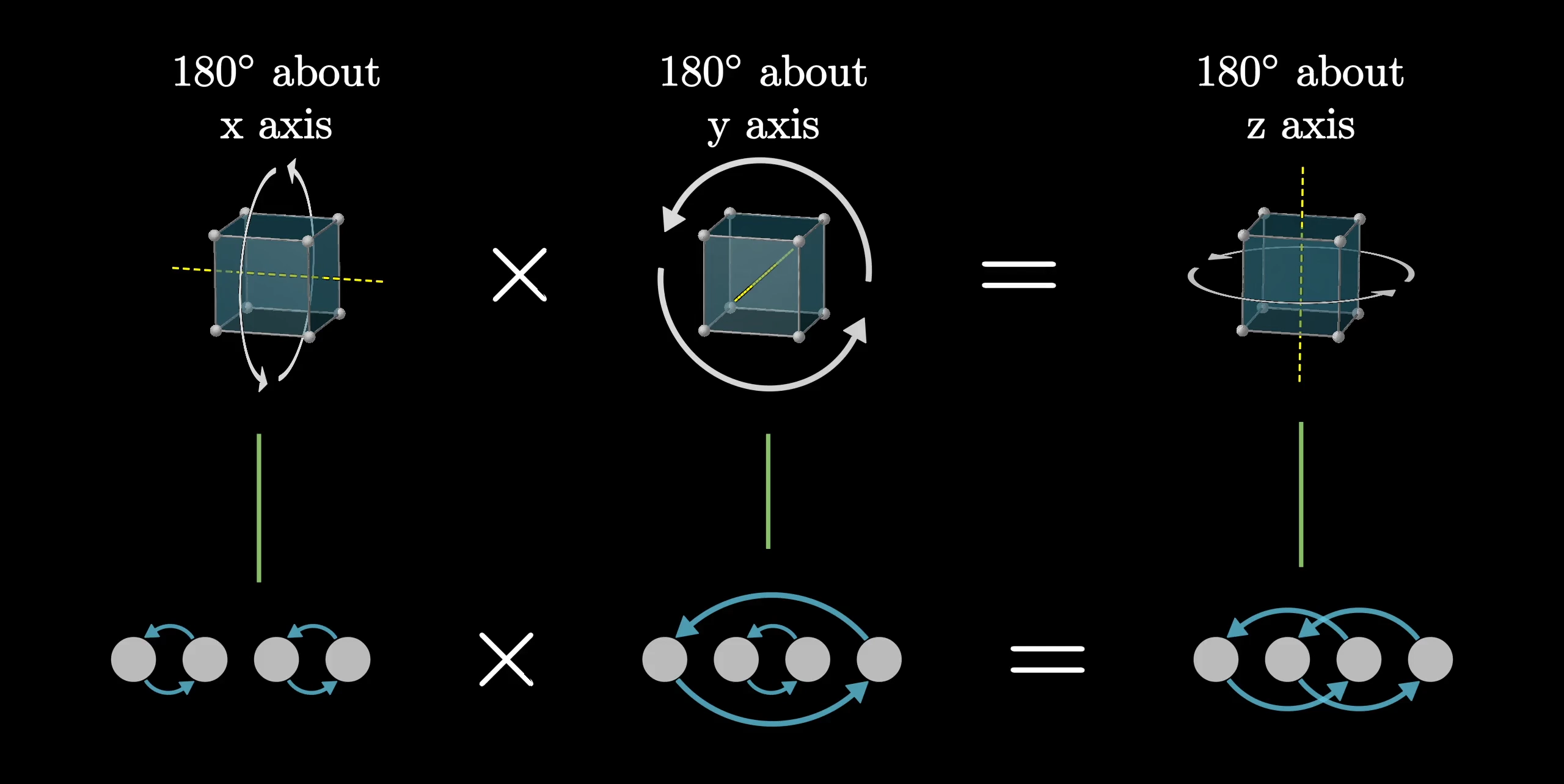
When you have a correspondence where this is true for all products, it's called an "isomorphism", which is maybe the most important idea in group theory. When two groups are isomorphic to each other, it means they have the same underlying structure. This particular isomorphism between cube rotations and permutations of four objects is a bit subtle, but for the curious among you, you may enjoy taking a moment to think hard about how the rotation of a cube permutes its four diagonals.
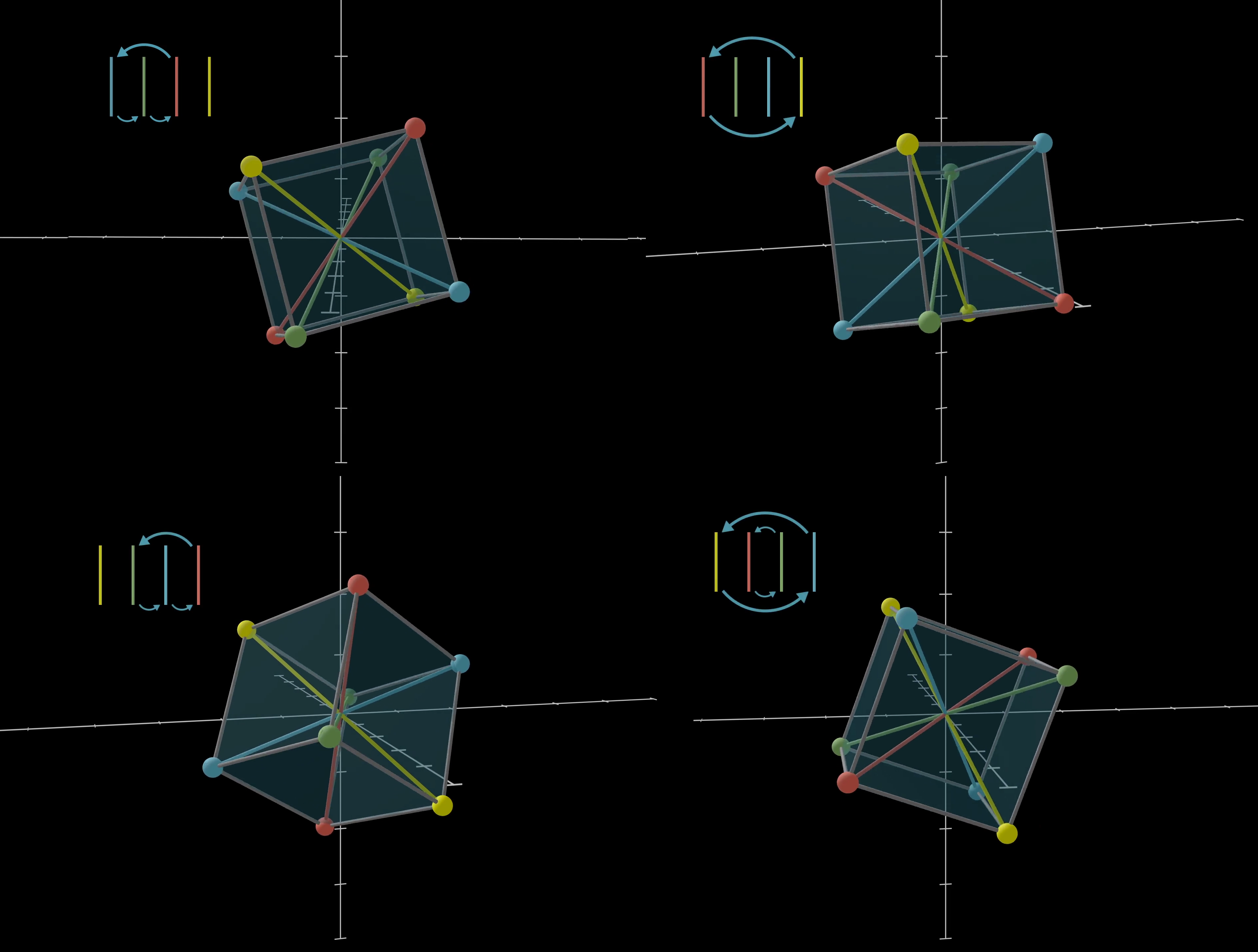
As you see more examples of a given group arising from seemingly unrelated situations, you'll get a sense for what group theory is all about. Think about how a number like 3 is not about any particular triplet of things, it's about all possible triplets of things.
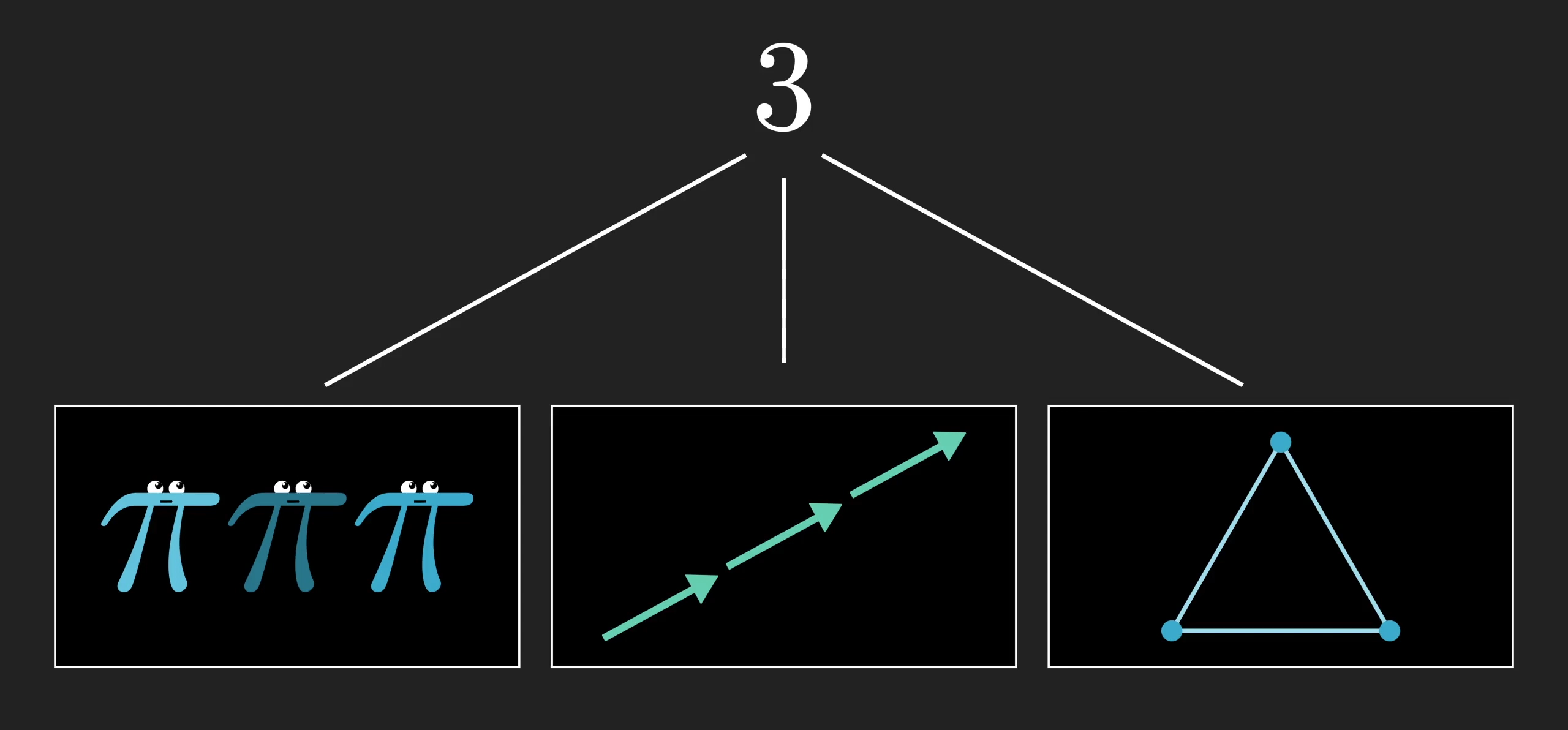
In the same way a group is not really about symmetries of a particular object, it's an abstract way that things even can be symmetric. There are even plenty of situations where groups come up in a way that doesn't feel like a set of symmetric actions at all, just as numbers can do much more than count. In fact, seeing the same group come out of different situations is a great way to reveal unexpected connections between distinct objects; that's a very common theme in modern math.
The Monster
An isomorphism between groups means they are describing the same structure. And once you understand this about groups, it leads you to a natural question, which will eventually lead us to the monster: What are all the groups? Now you're in a position to be a bit more sophisticated with this question: What are all the groups up to isomorphism, which is to say we consider two groups to be the same if there's an isomorphism between them. This is asking something more fundamental than what are all the symmetric things, it's a way of asking what are all of the ways that something can be symmetric? Is there some formula or procedure for producing them all? Some meta-pattern lying at the heart of symmetry itself?
This question turns out to be hard. Exceedingly hard.
To start, there are infinite groups, for instance the ones describing the infinite symmetries of a line or a circle. Then there are finite groups, like all the ones we've looked at up to this point. To maintain some hope of sanity, let's limit our view to finite groups. In much the same way that integers can be broken down in their prime factorizations, or molecules can be described based on the atoms within them, many groups also can be broken down as a kind of combination of smaller groups. The ones which can't be broken down any further, analogous to prime numbers or atoms, are known as the "simple groups".
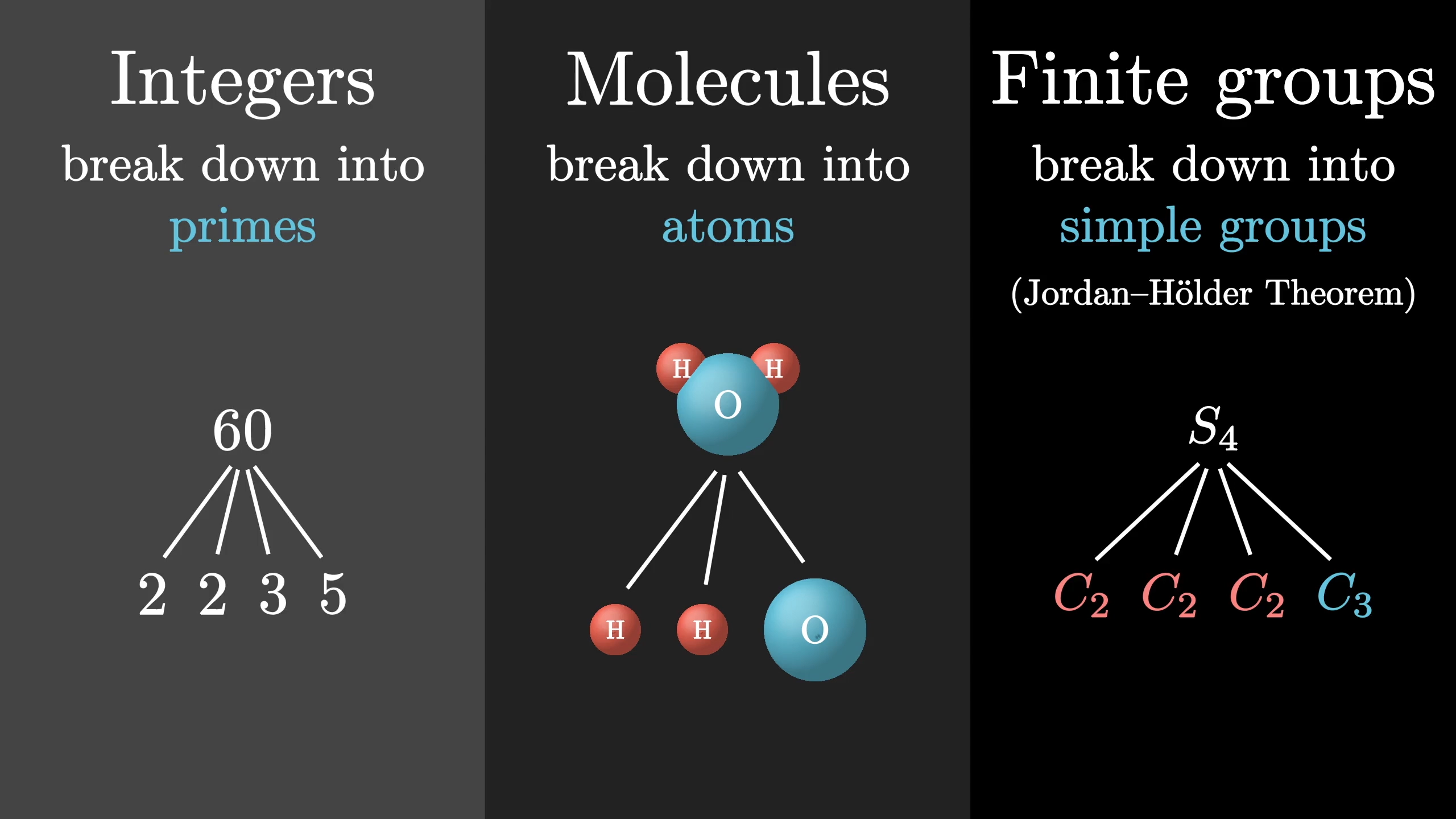
To give a hint as to why this is useful, remember how we said that group theory can prove that there's no formula for a degree-5 polynomial the way there is for quadratic equations? The way that proof looks like involves showing that if there were some kind of mythical quintic formula, something which uses only radicals and the basic arithmetic operations, then the permutation group on 5 elements would decompose into certain kinds of simple groups, known fancifully as cyclic groups of prime order. But the actual way it breaks down involves a different kind of simple group, one which polynomial solutions built up from radicals would never allow.
That's a super high level description, of course, with a semester's worth of details missing. But the point is that you have this highly non-obvious fact about a different part of math whose solution comes down to finding the atomic structure of a certain group. Which is all to say that understanding the nature of these simple groups, these atoms, actually matters.
You could think of the question of finding all the finite groups as breaking down into two steps: Find all the simple groups, and find all the ways to combine them. The first question is like finding the periodic table, and the second is a bit like doing all of chemistry thereafter.
The good news is that mathematicians have found all the finite simple groups. Well, more pertinent is that they proved how the ones they found are all the ones out there. It took many decades, tens of thousands of dense pages of advanced math, hundreds of some of the smartest minds out there, and significant help from computers, but by 2004 with a culminating 1,200-page paper to tie up loose ends, there was a definitive answer. Many mathematicians agree this was one of the most monumental achievements in the history of math.
The bad news is that this answer is absurd.
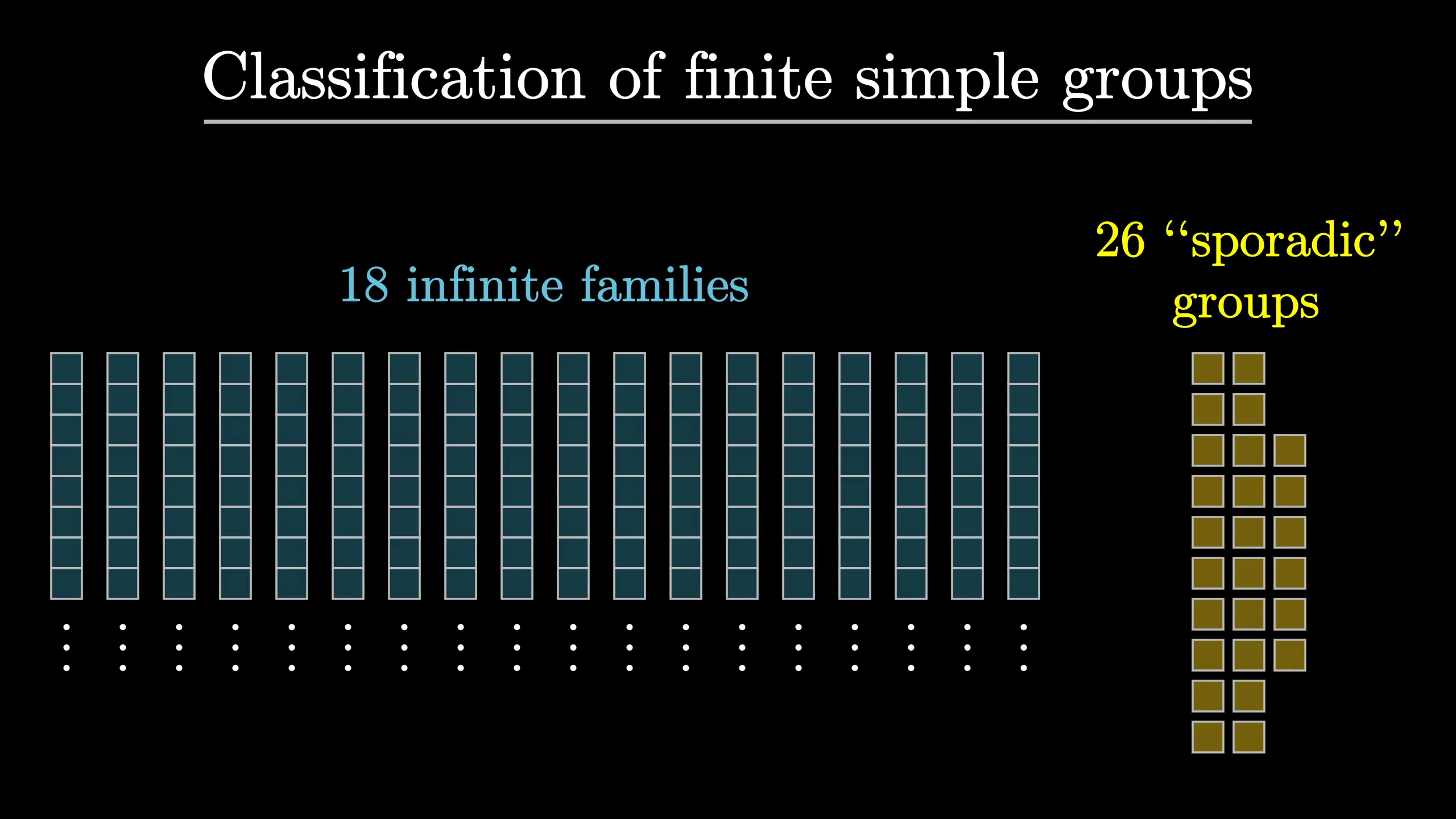
There are 18 distinct infinite families of simple groups, which makes it very tempting to lean into the periodic table analogy. However, groups are stranger than chemistry because there are also 26 simple groups just left over that don't fit the other patterns. These 26 are known as the sporadic groups. The realization that a field of study rooted in symmetry itself has such a patched together fundamental structure is… I mean it's just bizarre! It's like the universe was designed by committee.
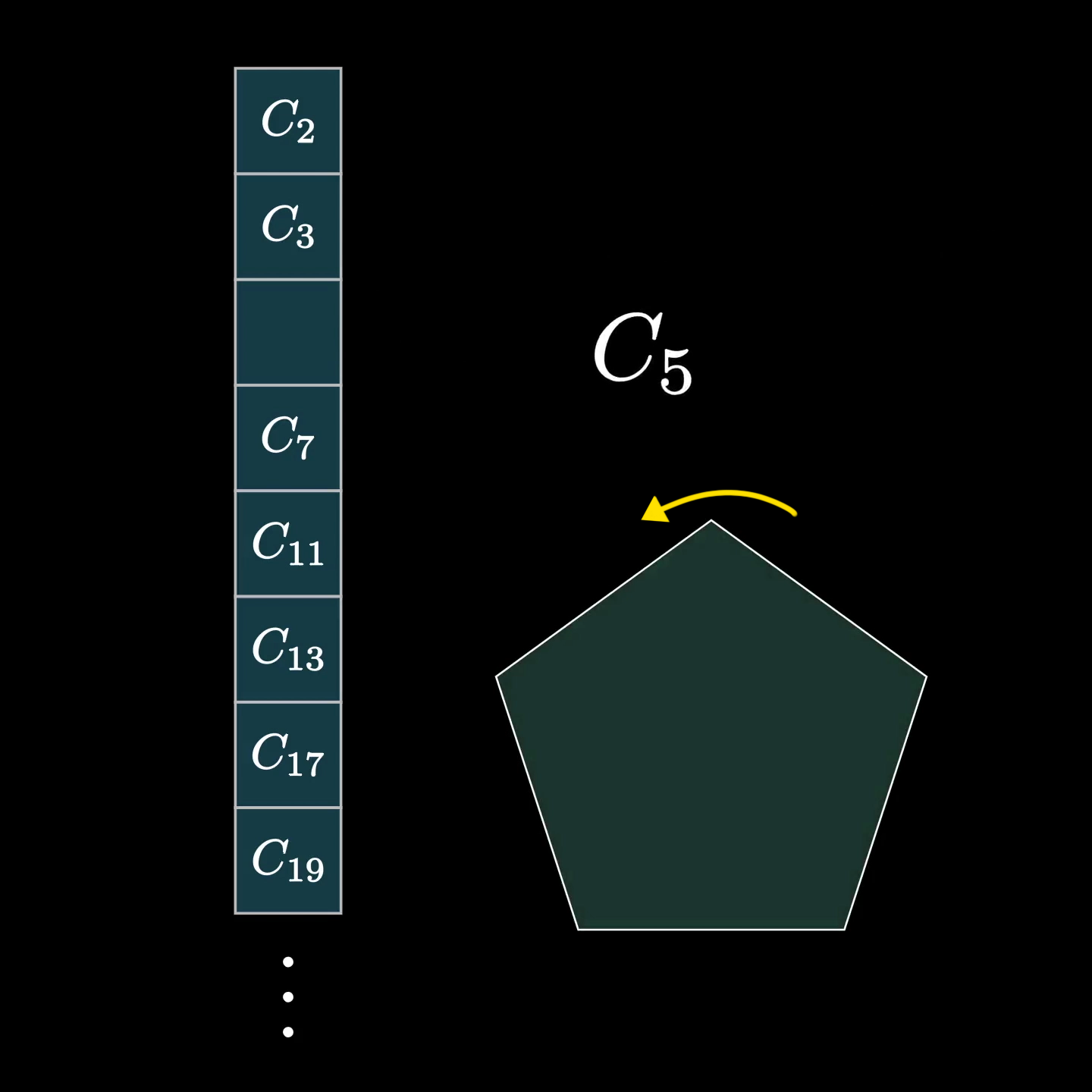
If you're wondering what we mean by an infinite family, one such family of simple groups includes all the cyclic groups with prime order. These are the symmetries of a regular polygon with a prime number of sides when you're not allowed to flip it over.
Another of these infinite families is very similar to the permutation groups we saw earlier, but there's the tiniest constraint on how they can shuffle n items. If they act on 5 or more elements, these groups are simple, which incidentally is heavily related to why polynomials with degree 5 or more often have solutions which can't be written down using radicals.
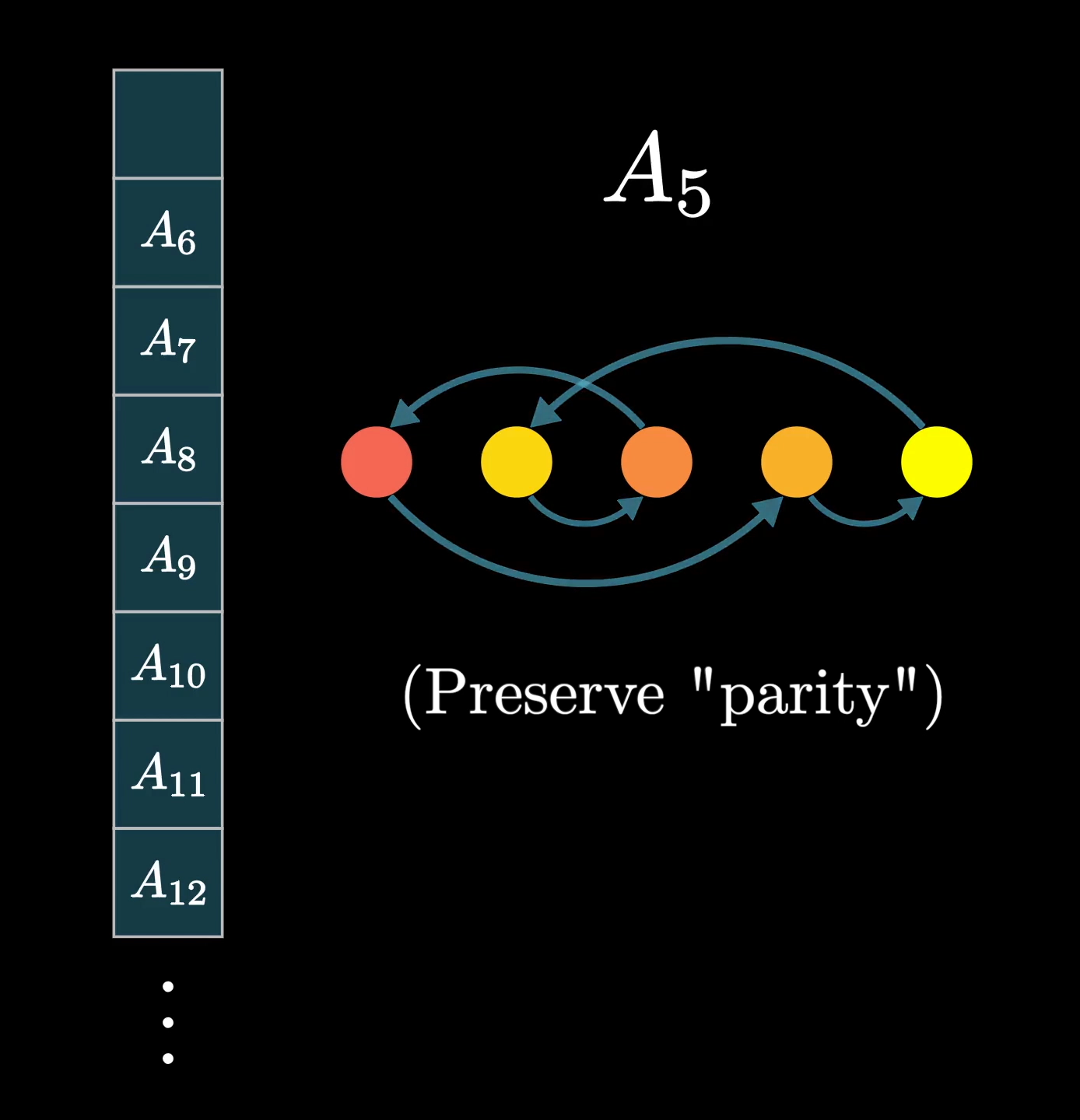
The others are notably more complicated, and I'm told that there's a little more ambiguity in how to organize them into cleanly distinct families without overlap. But everyone agrees that the 26 sporadic groups stand out as something very different.
The largest of these sporadic groups is known as the monster group, and its size is the number I mentioned at the start. The second largest, and I promise this isn't a joke, is known as the baby monster group. 19 of the sporadic groups are in some sense children of the monster, and the mathematician Robert Griess called these twenty the "happy family". He called the other 6, which don't even fit that pattern, the pariahs. As if to compensate for how complicated the underlying math here is, the experts really let loose on their whimsy while naming things.
Let me emphasize, having some group which is large isn't that significant. But the idea that the fundamental building blocks for one of the most fundamental ideas in math come in this collection that just abruptly stops around 8\times 10^{53}? That's weird.
In the same way that I introduced groups as symmetries, a collection of actions, you might wonder what the monster acts on. What object does it describe the symmetries of? There is an answer, but it doesn't fit into 2 or 3 dimensions to draw. Nor does it fit into 4 or 5. Instead, to see what the monster acts on we'd have to jump up to… 196,883 dimensions. Just describing one of the elements of this group takes around 4 gigabytes of data.
There are plenty of larger groups that have much smaller computational descriptions. The permutation group on 101 elements was dramatically larger, but we could describe each element with very little data, for example a list of a hundred numbers.
No one really understands why the sporadic groups, and the monster in particular, are there. Maybe in a few decades, there will be a clearer answer, maybe one of you will come up with it, but despite knowing that they're deeply fundamental to the structure of math, and arguably to physics, a lot about them remains mysterious.
In the '70s, mathematician John McKay was making a switch to studying group theory to an adjacent field, and he noticed a number very similar to that 196,883 we just saw, but in a completely unrelated context. A number 1 bigger than this was in the series expansion of a fundamental function in a very different part of math, relevant to these things called modular forms and elliptic functions.
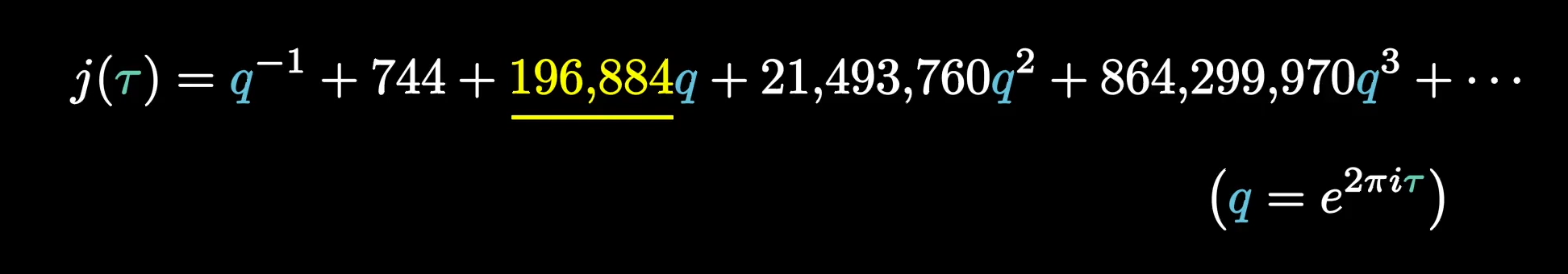
Assuming this was more than a coincidence seemed crazy, enough that it was playfully deemed "moonshine" by John Conway. After more numerical coincidences like this one were noticed, it gave rise to what is now known as the monstrous moonshine conjecture. The whimsical names just don't stop! This was proved by Richard Borcherds in 1992, solidifying a connection between very different parts of math that at first glance seemed unrelated. 6-years later, by the way, he won the Fields Medal, in part for the significance of this proof.
There are even connections between the monster and string theory. Maybe it shouldn't be surprising that something which arises from studying symmetry itself is relevant to physics, but in light of how random the monster seems at first glance, the connection still elicits a double-take.
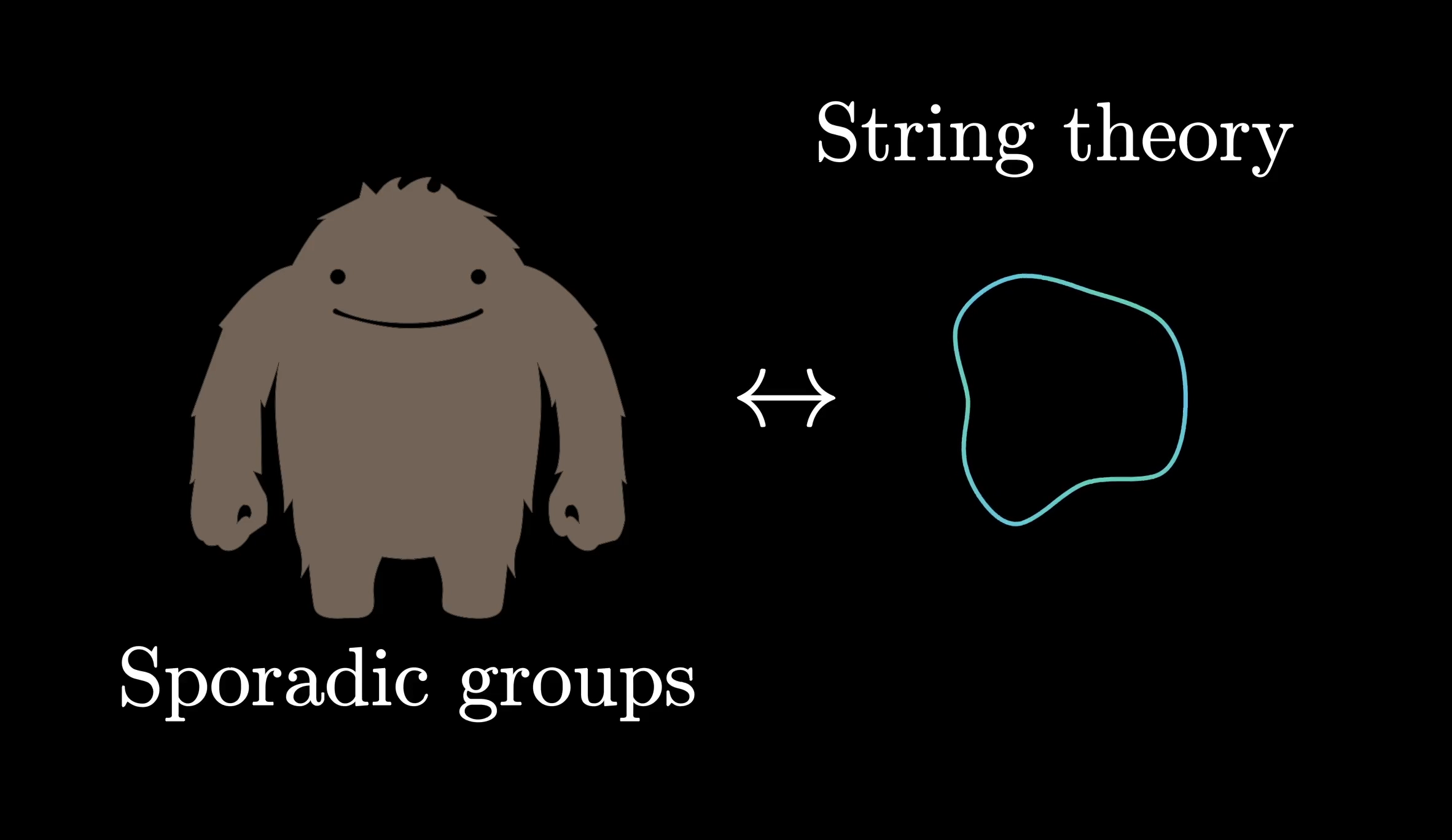
To me, the monster and its absurd size is a nice reminder that fundamental objects are not necessarily simple. The universe doesn't really care if its final answer looks clean; they are what they are by logical necessity, with no concern over how easily we'll be able to understand them.
The axioms for a group are short and natural... Yet somehow hidden behind these axioms is the monster simple group, a huge and extraordinary mathematical object, which appears to rely on numerous bizarre coincidences to exist. The axioms for groups give no obvious hint that anything like this exists.
– Richard Borcherds
Thanks
Special thanks to those below for supporting this lesson.