How secure is 256 bit security?

What is 256 bit security?

If a protocol is described as having "$n$-bit security", it means an attacker would have to run some computation $2^n$ times to break the system.

For example, the last post touched on the function SHA256, which takes in an input of arbitrary length, and produces an output which is always 256 bits long. It's believed that this is a crytographic hash function, which means that it's computationally infeasible to reverse it. More specifically, if you want to find an input producing a particular output, there is no better method than to repeatedly guess and check.

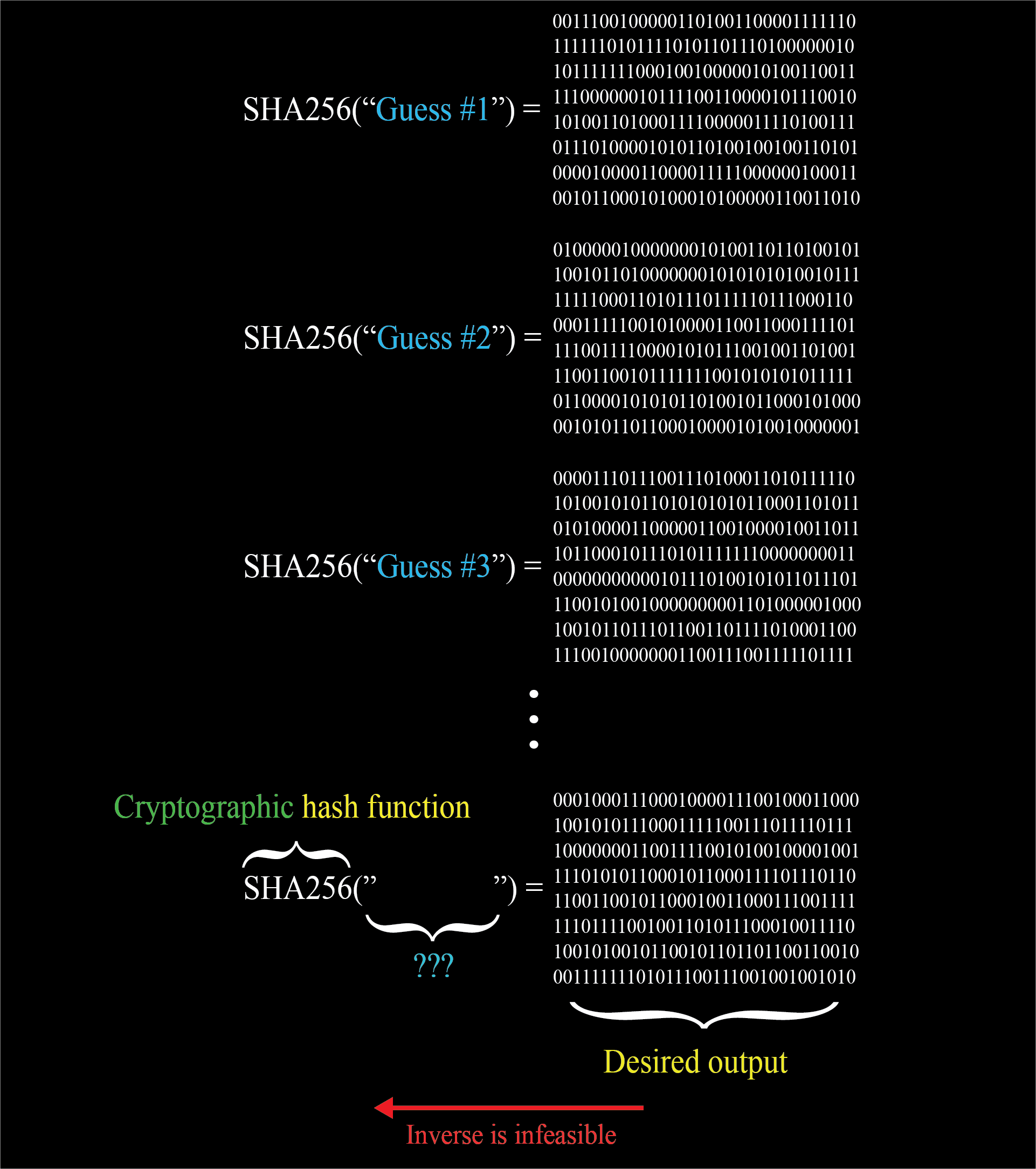
These cryptographic hash functions are used, for example, to store passwords without revealing what those passwords are. If your database stores usernames and the associated hash of the corresponding password, then when a user enters their password, you can check if it’s correct by computing its hash and comparing it with what is stored. But anyone looking at the database should have no way to reverse engineer what the passwords are. ¹

A core theme of cryptography is to find tasks which are easy in one direction but hard in another, so it should make sense that these one-way hash functions are a very common building block in all sorts of security protocols, including not just password storage, but digital signatures, proofs of work, and many more. So how hard is this guess-and-check process, exactly? The outputs of this hash function behave like a random sequence of numbers, so it’s helpful to think of rolling a die.

For SHA256, there are not six possible outputs, there are $2^{256}$. So on average it will take $2^{256}$ guesses to find an input with a particular hash². But how difficult is this, exactly? A number like $2^{256}$ is so far removed from anything we ever deal with that it can be hard to appreciate its size. Nevertheless, let’s give it a try.

Appreciating Large Powers of Two

The human mind is best at breaking down concepts into smaller pieces to analyze. $2^{256}$ is $2^{32}$ multiplied by itself eight times. $2^{32}$ is about 4 billion, which is a number we can at least start to think about, so all we need to do is appreciate what multiplying 4 billion times itself eight successive times feels like.

4 Billion Hashes Per Second

The GPU on your computer can let you run parallel computations incredibly quickly. If you specially program a GPU to run a cryptographic hash function over and over, a really good one can do just under a billion hashes per second.

Let’s say you cram a computer with extra GPUs so that it can guess and check 4 billion times per second. So our first 4 billion is the number of hashes per second per computer.

4 Billion Computers

Now picture 4 billion of these GPU-packed computers. For comparison, even though Google does not make the number of servers it runs public, estimates have it somewhere in the single-digit millions.

In reality, most of those servers are much less powerful than our imagined GPU-packed machine, but if Google replaced all its millions of servers with machines like this, 4 billion machines would mean about 1,000 copies of this souped-up Google, which I’ll call one KiloGoogle++.

4 Billion KiloGoogles

There are about 7.9 billion people on Earth, so imagine giving a little over half the people on Earth their own personal KiloGoogle.

4 Billion Earths

Now imagine 4 billion copies of this Earth. The Milky Way has between 100 and 400 billion stars, so this would be akin to 1% of all stars in the galaxy having a copy of Earth, where half the population on each has their own personal KiloGoogle.

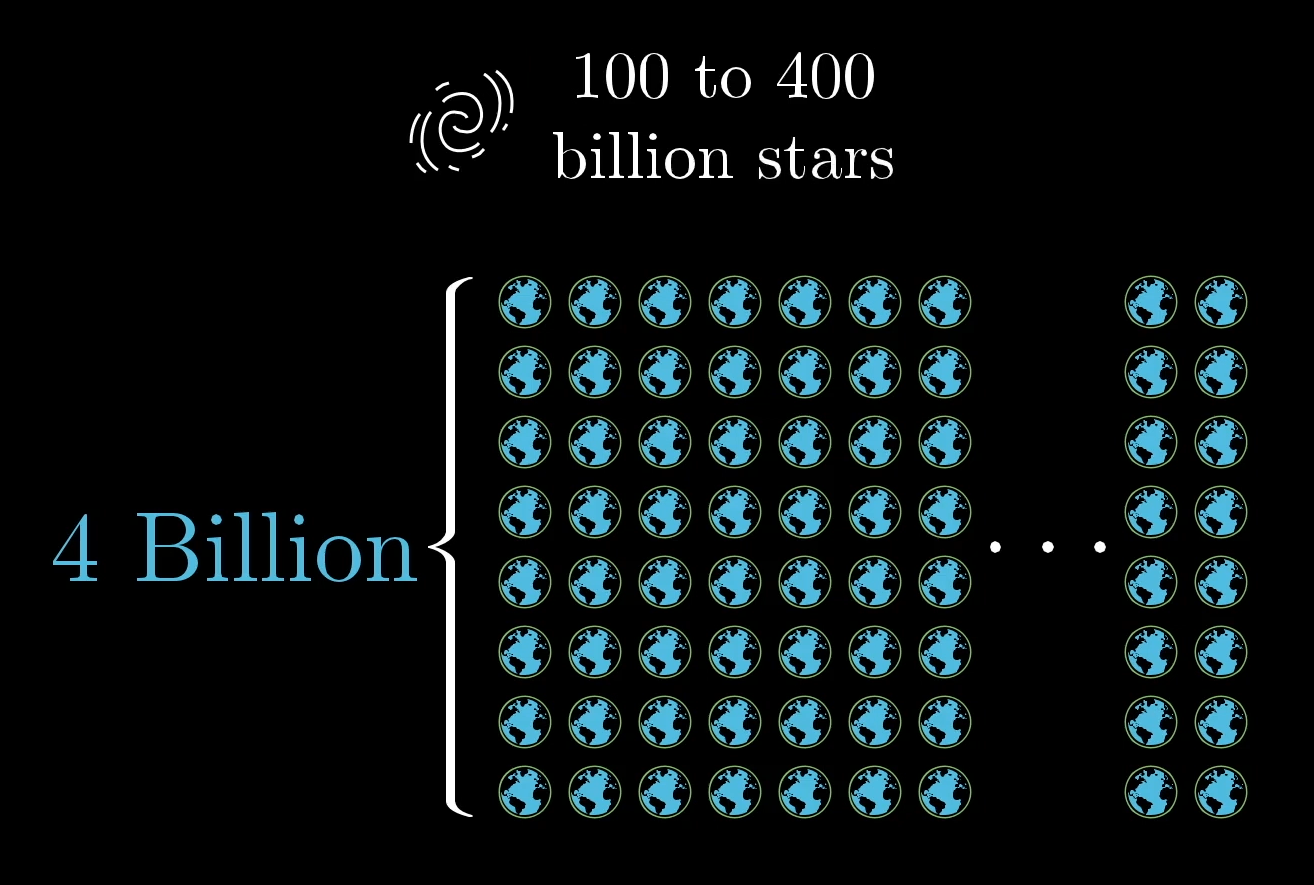
4 Billion Milky Ways

Now picture 4 billion copies of the Milky Way, and call this your GigaGalactic Super Computer, running $(2^{32})^5 = 2^{160}$ guesses per second.

4 Billion Seconds

4 billion seconds is about 126 years, which is still a reasonable amount of time to want to keep something hidden. Maybe you’re hiding a digital treasure for your great-great-great grandchildren!

4 Billion Seconds Squared

4 billion times 126 years is about 507 billion years. This is roughly 37 times the age of the universe. The Earth will have been swallowed up by the sun a long time before this, hopefully nobody cares about your password anymore.

1 in 4 Billion Success Rate

So even if you were to have your GPU-packed KiloGoogle-per-person multi-planetary GigaGalactic Super Computer guessing numbers for 37 times the age of the universe, it would still only have a 1 in 4 billion chance of finding a correct guess.

Modern Bitcoin Hashing

In 2021, all the miners put together make guesses at a rate of about 100 billion billion ($10^{20}\approx 2^{66}$ ) hashes per second. Which is four times more than what was described as a KiloGoogle.

This is not because there are actually billions of GPU packed machines out there, but because miners use something about ten thousand times better than a GPU: Application-Specific Integrated Circuits.

These are pieces of hardware specifically designed for bitcoin mining and nothing else. It turns out that there are a lot of efficiency gains to be had when you throw out the need for general computation, and design your integrated circuits for a single, specific task.