But how does bitcoin actually work?
The majority of what you will find online about Bitcoin is centered on price fluctuations, speculations about the future of finance, and memes about both.
This article is not about any of that. The story today is about how the invention of bitcoin was the solution to an interesting mathematical puzzle, and how that solutions offers a window into some clever ideas from cryptography like digital signatures and cryptographic hash functions.
We’re going to walk step-by-step through how you might have invented your own version of Bitcoin. By the end, you should have an understanding of how Bitcoin works, and where there’s room for different design choices, hence the entire ecosystem of alternate cryptocurrencies.
One point worth stressing, by the way, is that even though you and I will dig into the underlying details here, you don’t actually need to know those details to use a cryptocurrency, just like you don’t need to know the details of what happens under the hood when you swipe a credit card. Like any other digital payments, there are plenty of user-friendly applications that let you send and receive these currencies very easily.
Just like with traditional banking, it’s possible to use cryptocurrencies like Bitcoin without needing to understand everything that’s going on underneath.
What's the puzzle
No one knows who invented Bitcoin. The paper describing it, and the initial code offering an implementation, were published under the pseudonym Satoshi Nakamoto shortly after the 2008 financial crisis.
This timing was likely no coincidence, since the premise of a cryptocurrency is to offer a way for people to make transactions without relying on a central point of trust. Usually when you use your credit card to pay for goods, there's a bank (or set of banks) that must be trusted to correctly reduce from your account and add to the recipient's. Most currency is issued by a government, which then has some level of control over that currency, say by affecting the money supply. This means holders of that currency are placing some amount of trust in the government issuing it to manage it well.
The intent of bitcoin was to circumvent both of these. It was conceived of as a currency controlled by no one, with a money supply no one could change, where it's possible for one party to pay another and know that the books are balanced properly without relying on a central point of trust.
Some readers may question whether or not this kind of decentralization is valuable, or necessary, and if so how much. Those are worthy questions, but entirely irrelevant to our discussion today. Whether or not you feel a personal need for trustless payments, the question of whether or not such a system is possible is a technologically interesting one.
Cryptography is a field originally developed to encrypt messages, involving some incredibly deep math to do so. Just as there is a famous "unreasonable effectiveness of mathematics", the tools of cryptography have a similarly unreasonable effectiveness beyond the scope of secret messages, with the challenge of creating a decentralized currency serving as just one example.
Inventing Cryptocurrency
To begin, set aside the thought of cryptocurrencies for a few minutes. We’re going to start the story with something more down to earth: Ledgers and digital signatures.
If you and your friends exchange money pretty frequently, paying your share of the dinner bill and such, it can be inconvenient to exchange cash all the time. So you might decide to keep a communal ledger where you can record payments as if they took place with real cash, reminding yourselves of what payments need to be made whenever you do decide to settle up.
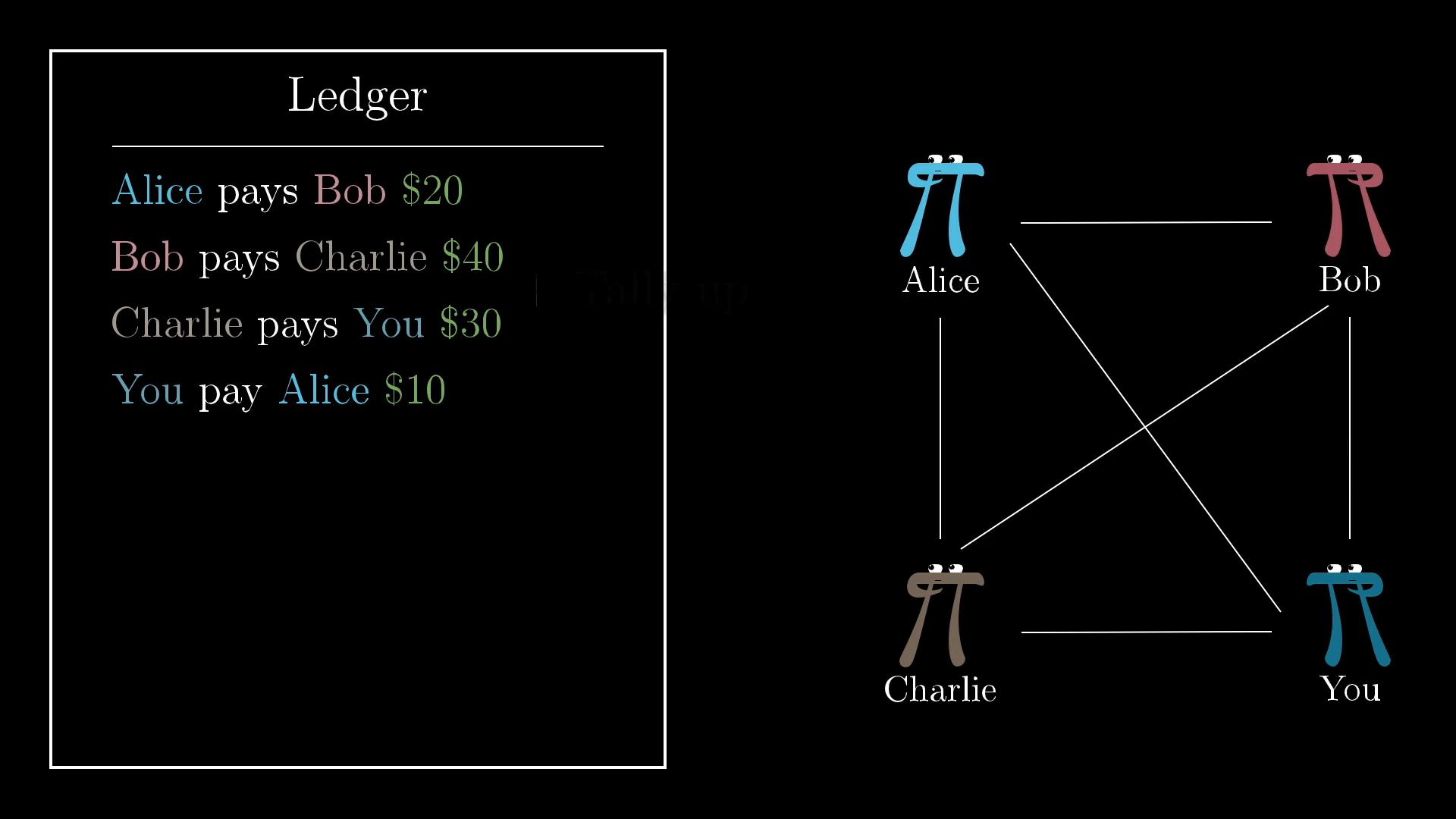
A ledger is just a list of transactions, used to keep track of everyone’s balance.
This ledger will be something public and accessible to everyone, like a website where anyone can go and add new lines.
At the end of every month, say, you could all look through the list of transactions and tally everything up. If you’ve spent more than you received, you put that money into the pot, and if you’ve received more than you spent, you take that money out.
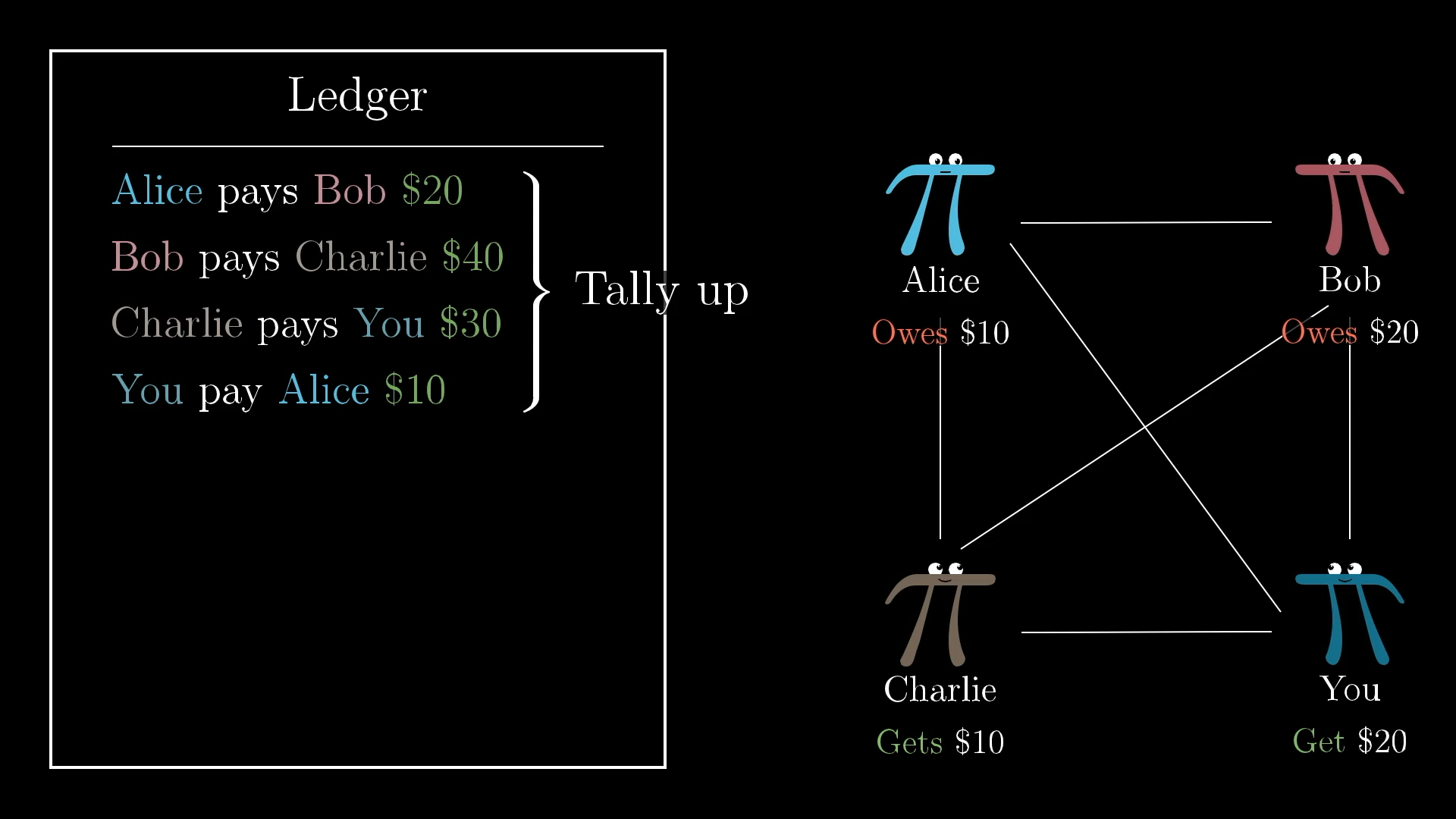
So the protocol for being part of this system looks something like this:
- Anyone can add lines to the ledger.
- At the end of every month, everyone gets together to settle up with real money.
Of course, there's a glaring problem with a public ledger like this where anyone can add a line. What’s to prevent Bob from going in and writing “Alice pays Bob $100” without Alice approving?
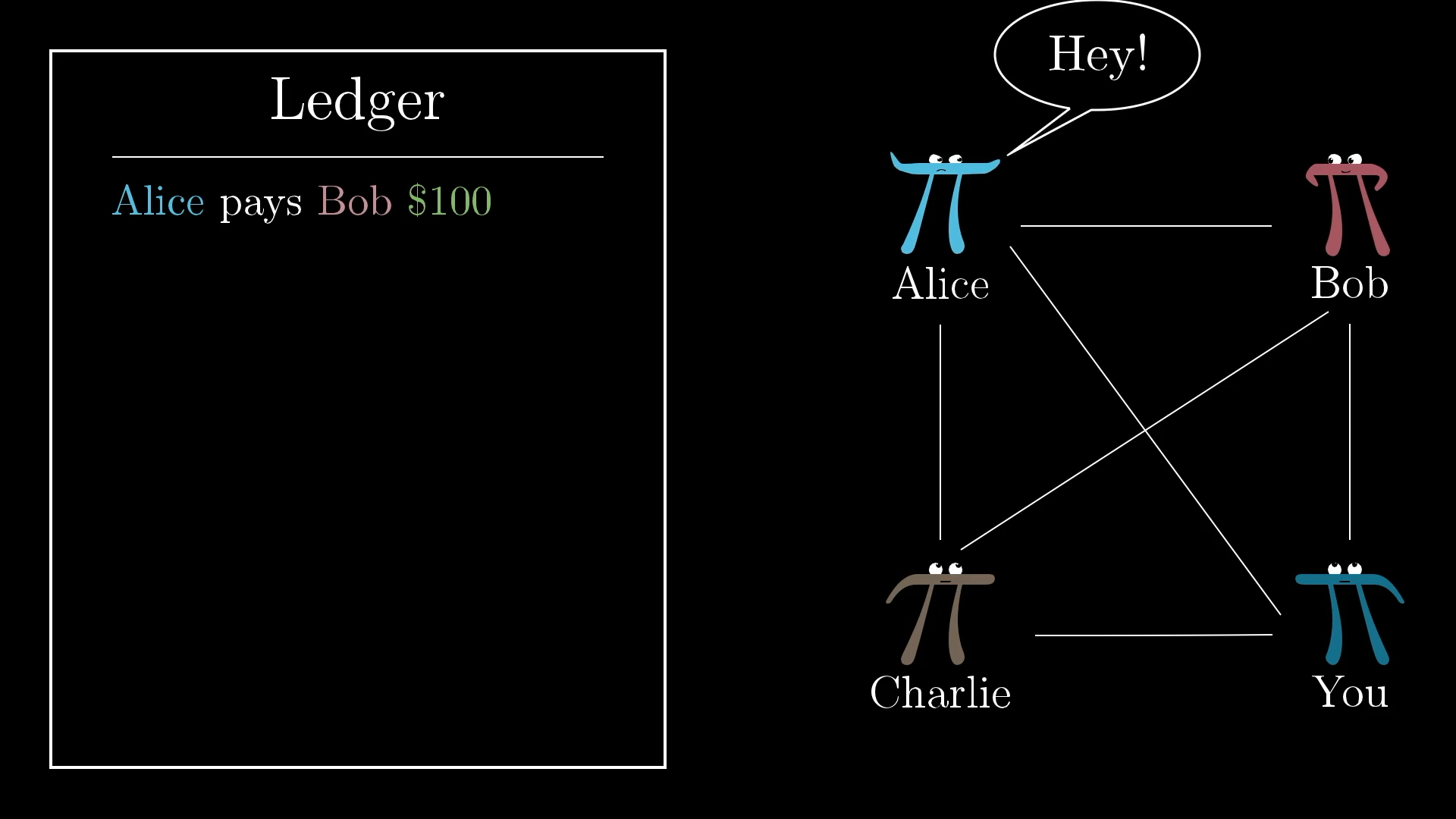
On this public ledger, anyone can write any transaction they want.
How are we supposed to trust that all these transactions are what the sender meant for them to be? This is where the first bit of cryptography comes in: Digital signatures.
Digital Signatures
Like a handwritten signature, the idea here is that Alice should be able to add something next to a transaction that proves that she has seen it, and approved of it. And it should be infeasible for anyone else to forge her signature.
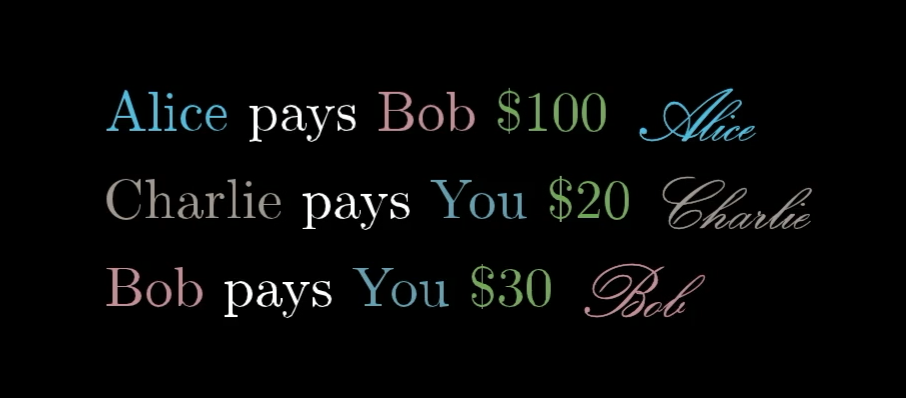
Can we add signatures to each line to verify that the transaction is approved by the sender?
At first it might seem like digital signatures shouldn't even be possible. Even if Alice is the only one able to create her signature initially, if it's just a set of 1's and 0's, shouldn't anyone be able to copy it thereafter? What's to prevent forgeries?

Forgeries are a problem in the real world because your handwritten signature always looks the same, so forging a signature just means copying it from one document to another. Digital signatures work differently. When Alice signs a statement, that signature is a function of two things:
- Some private information which only Alice has, known as her "private key"
- The message she is signing.
So Alice’s signature might be 00111010... on one document, but 11101001... on another. Both signatures are proof that Alice saw and approved of the document, but they aren't identical.
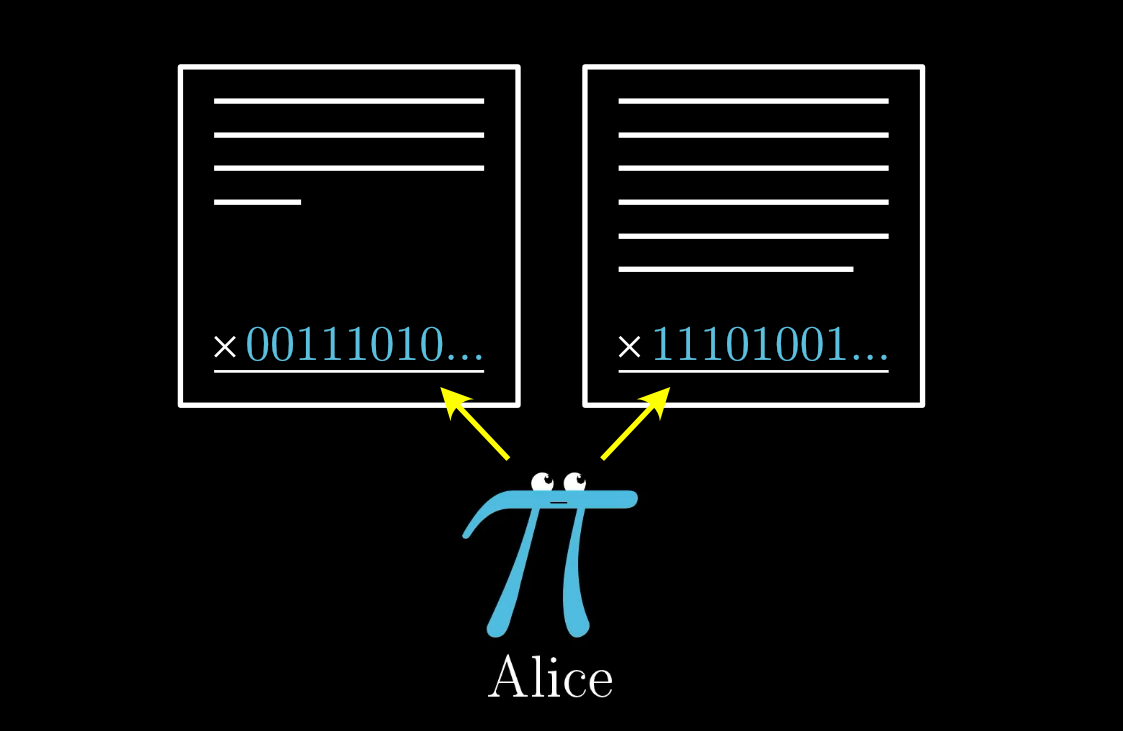
Alice signs each document differently depending on its content. But both signatures are hers.
But a signature function is only useful if there's a corresponding function to verify that it's valid.
The way this works is that everyone generates what’s called a public key/private key pair, each of which looks like some string of 1's and 0's. The private key is sometimes also called the “secret” key, so that we can abbreviate it to sk while abbreviating the public key as pk. As the names suggest, the secret key is something you should keep to yourself.
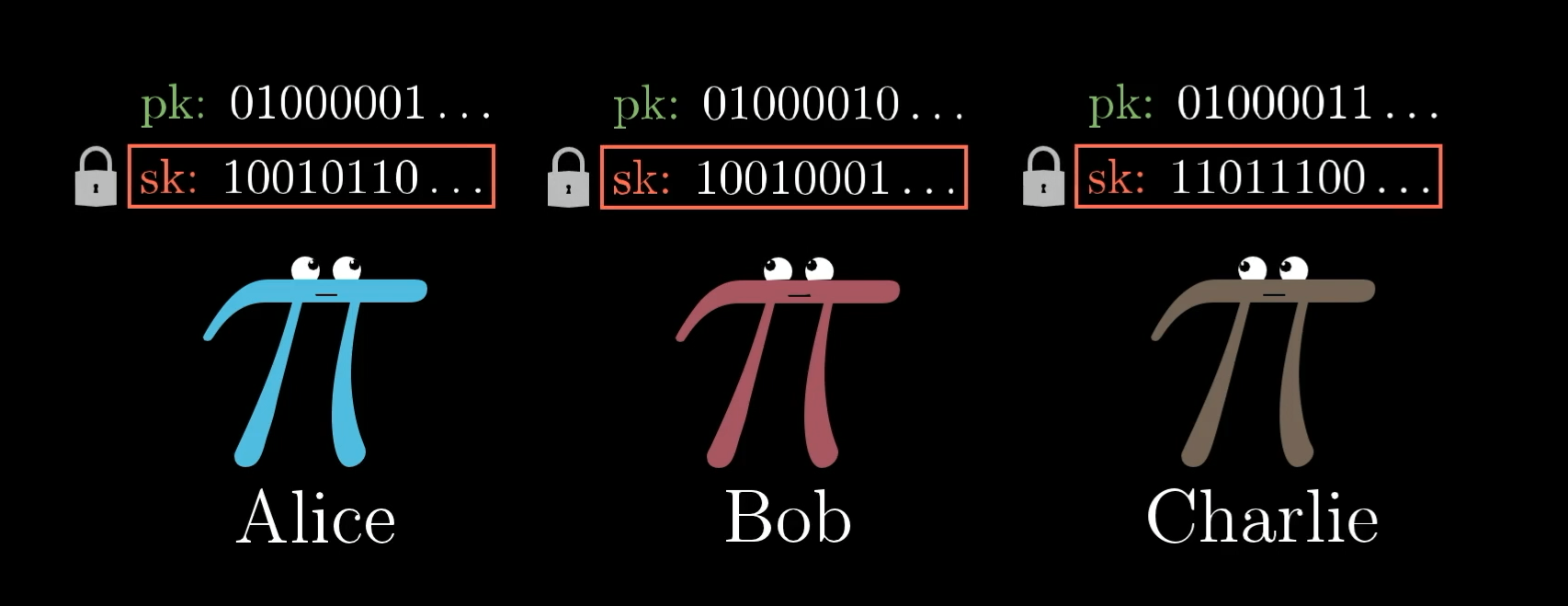
Each person gets their own public key and secret key.
Any digital signature scheme will consist of two functions, one to produce a signature on a message, and another to verify that a signature is valid.
Notice, the signing function requires using the secret key. The goal is that if Alice is the only one who knows her secret key, then only she is able to produce a signature. If that key is compromised, all bets are off.
The function is a way of asking "Was this signature on this message produced using the secret key associated with this public key?" It should return when applied to a valid signature, and to all other signatures.
Of course, so far I've said nothing about how these two functions and actually work. For this article we won't go into the details, which involve quite a bit of mathematical cleverness, but it would be worth you pausing to contemplate what properties you want it to have.
The hope is that producing a valid signature requires knowing the secret key, but there is, inevitably, one other way to produce a valid signature. Because everyone knows the public key, someone could run the function over and over on different potential signatures until one finally returns true.
For the digital signature scheme which Bitcoin uses, there are possible signatures. It's hard to overstate just how many this is. To call it astronomically large would be giving too much credit to astronomy. In fact, I made a supplemental lesson devoted just to illustrating what a huge number this is.

Let’s just say that when you verify a signature against a given message and public key, you can feel extremely confident that it was not produced using a guess-and-check method with the function. And what makes a digital signature algorithm a good one is if there's no way other than this guessing-and-checking that someone could forge a signature.
Copying the same line
So, returning to our ledger, we now have a way to sign transactions to verify that the sender approves.

This is all well and good. Any new transaction on the ledger needs to be signed, and the only way to sign it is by knowing the secret key. The signature changes based on the content of the transaction, so copying signatures from one transaction to another won’t work.
But there’s one problem here. Suppose Alice signs a transaction like “Alice pays Bob $100.” Bob can’t forge Alice’s signature on new messages, but he could just copy that same line as many times as he wants, since the message/signature combination is still valid.
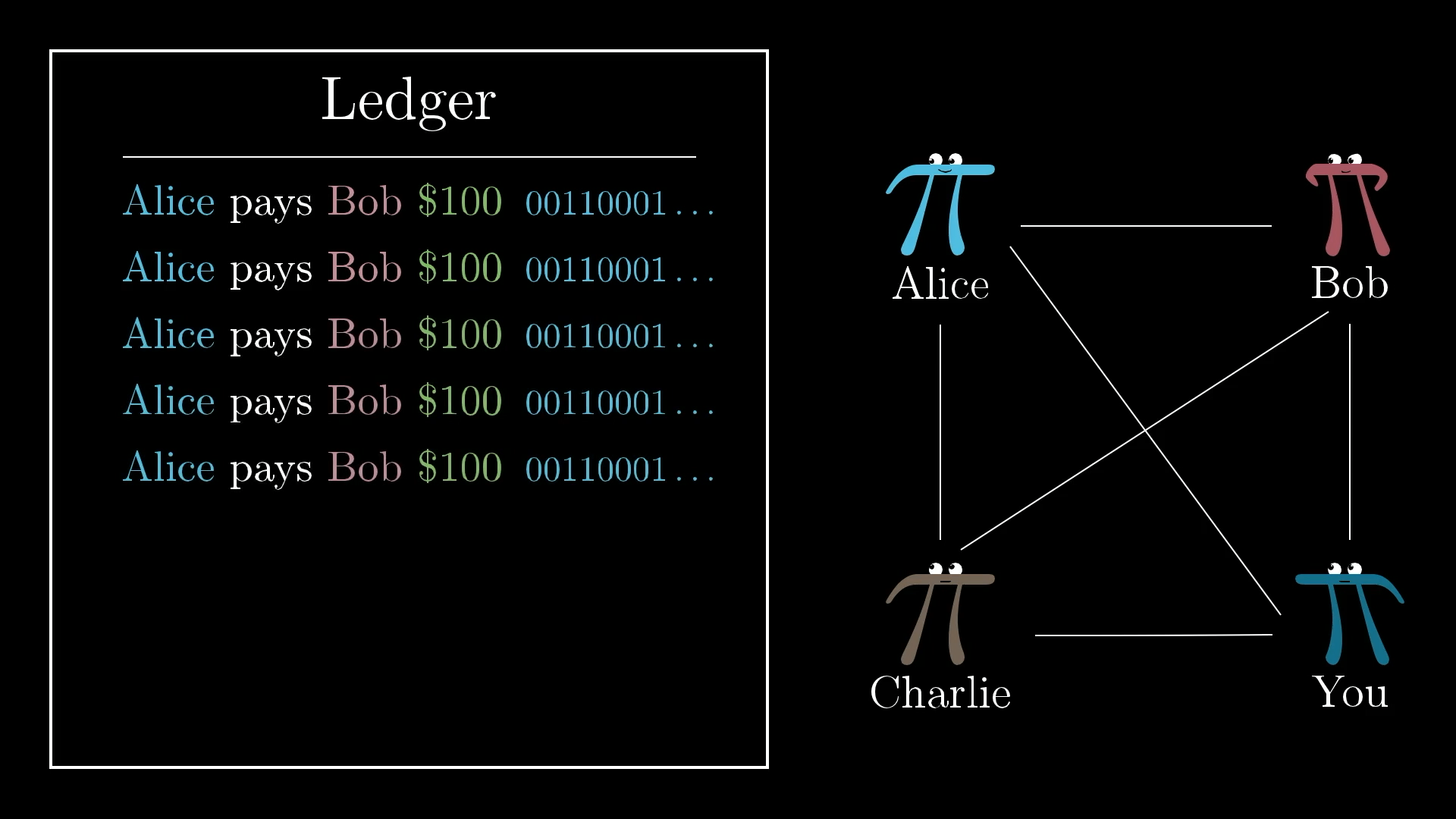
Anyone can create copies of previous transactions.
To solve this, we make it so that when you sign a transaction, the message has to include some unique ID associated with that transaction. That way, if Alice pays Bob $100 multiple times, each transaction requires a completely new signature.
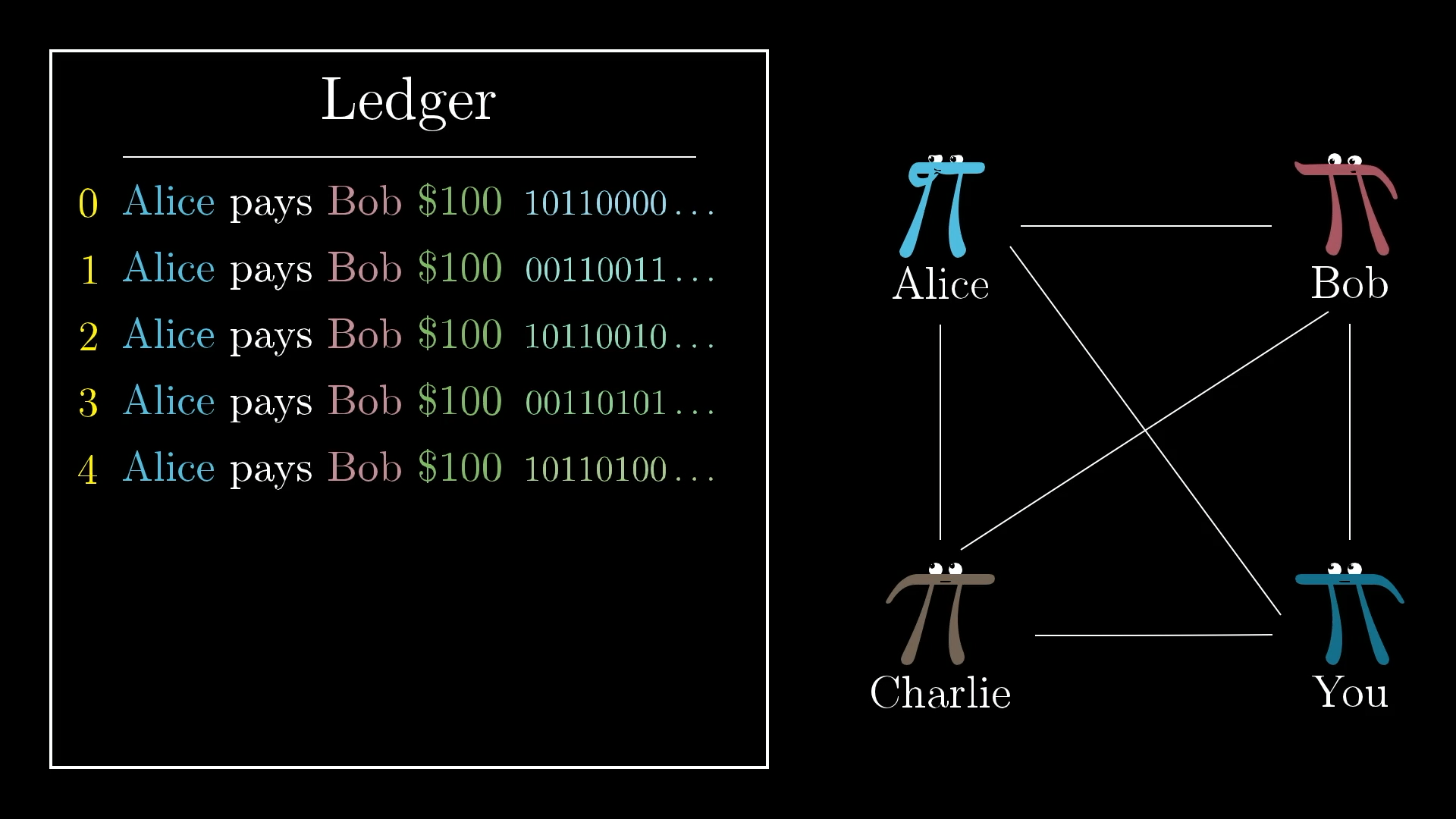
With these unique IDs, every new transaction must get a new signature, even if it’s otherwise identical to a previous transaction.
And with that, we have working digital signatures, which remove a huge aspect of trust in our initial protocol.
Removing Cash
But even still, this relies on an honor system of sorts. You’re trusting that everyone will actually follow through and settle up in cash at the end of each month. What if, for example, Charlie racks up thousands of dollars in debt, and then refuses to show up?
The only real reason to revert to cash to settle up is if some people (I’m looking at you Charlie) owe a lot of money. As long as nobody falls into debt, the ledger alone works fine. You never actually have to settle up in cash as long as you have some way to prevent people from spending too much more than they take in.
You don't actually need to settle up...

One thing you and your friend could do is have everyone pay $100 into the pot, and have the first few lines of the ledger read Alice gets $100, Bob gets $100, etc.
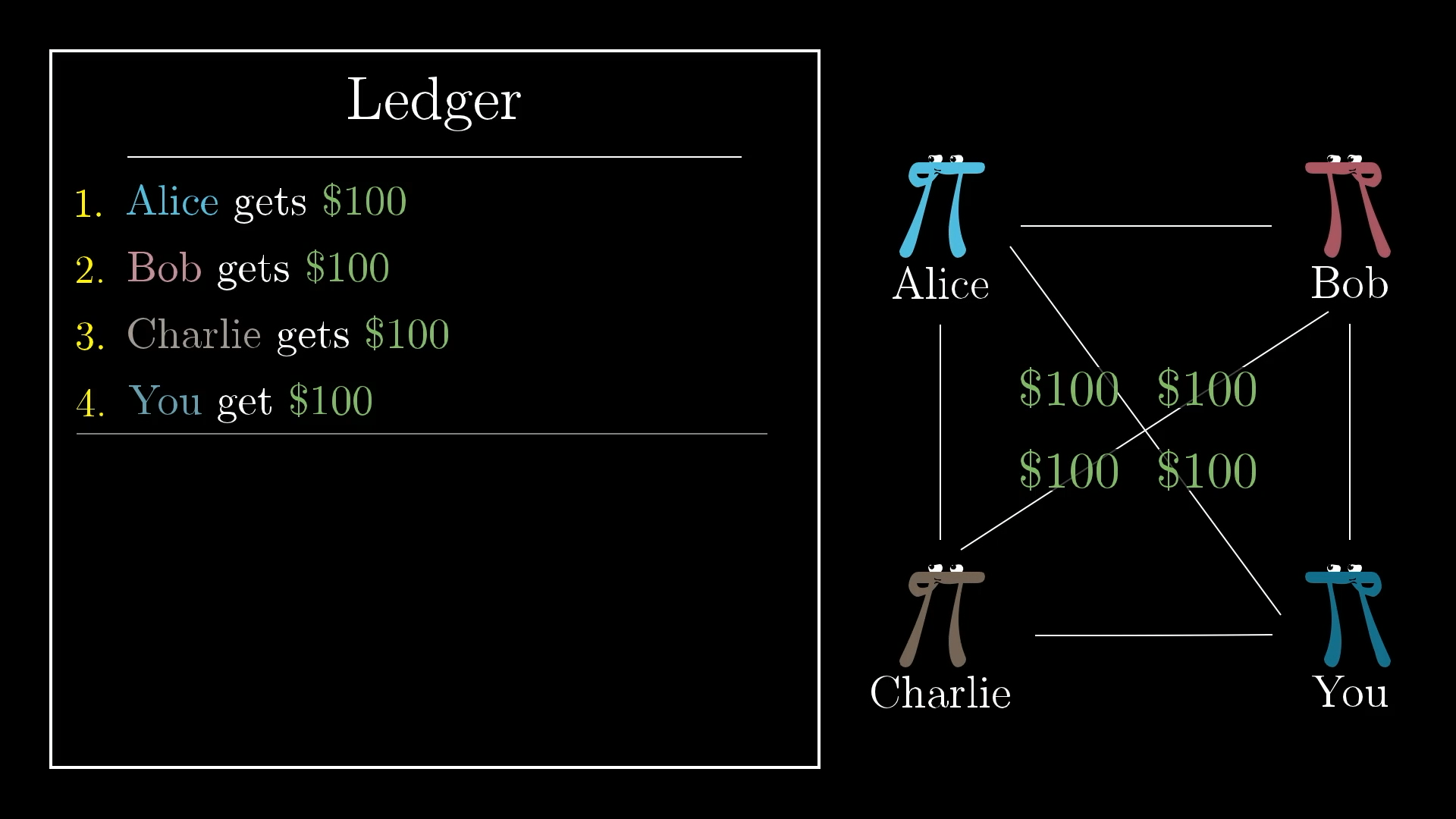
Everyone puts $100 in the pot to start.
Now, just don’t accept transactions when someone is spending more than they have on the ledger. For example, after starting everyone off with $100, if the first two transactions are (Charlie pays Alice $50 and Charlie pays Bob $50), then if he were to try to add Charlie pays You $20, readers of the ledger would recognize this as being invalid.
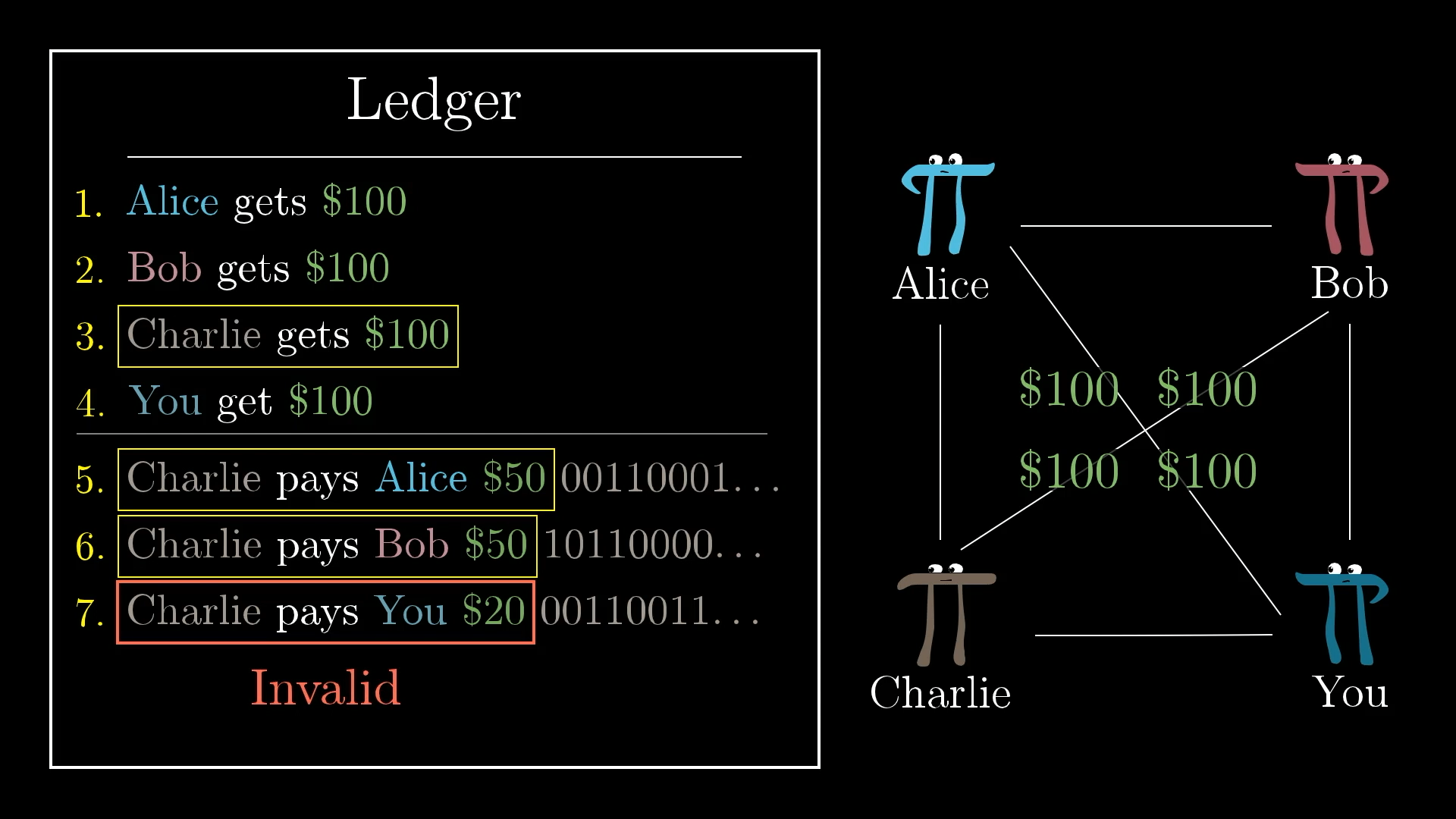
In this new system, we don’t allow people to spend more than they have.
Notice, this means that you now need to know the entire history of transactions just to verify that a new one is valid. (This is going to be mostly true for cryptocurrencies as well, though there is room for optimization.)
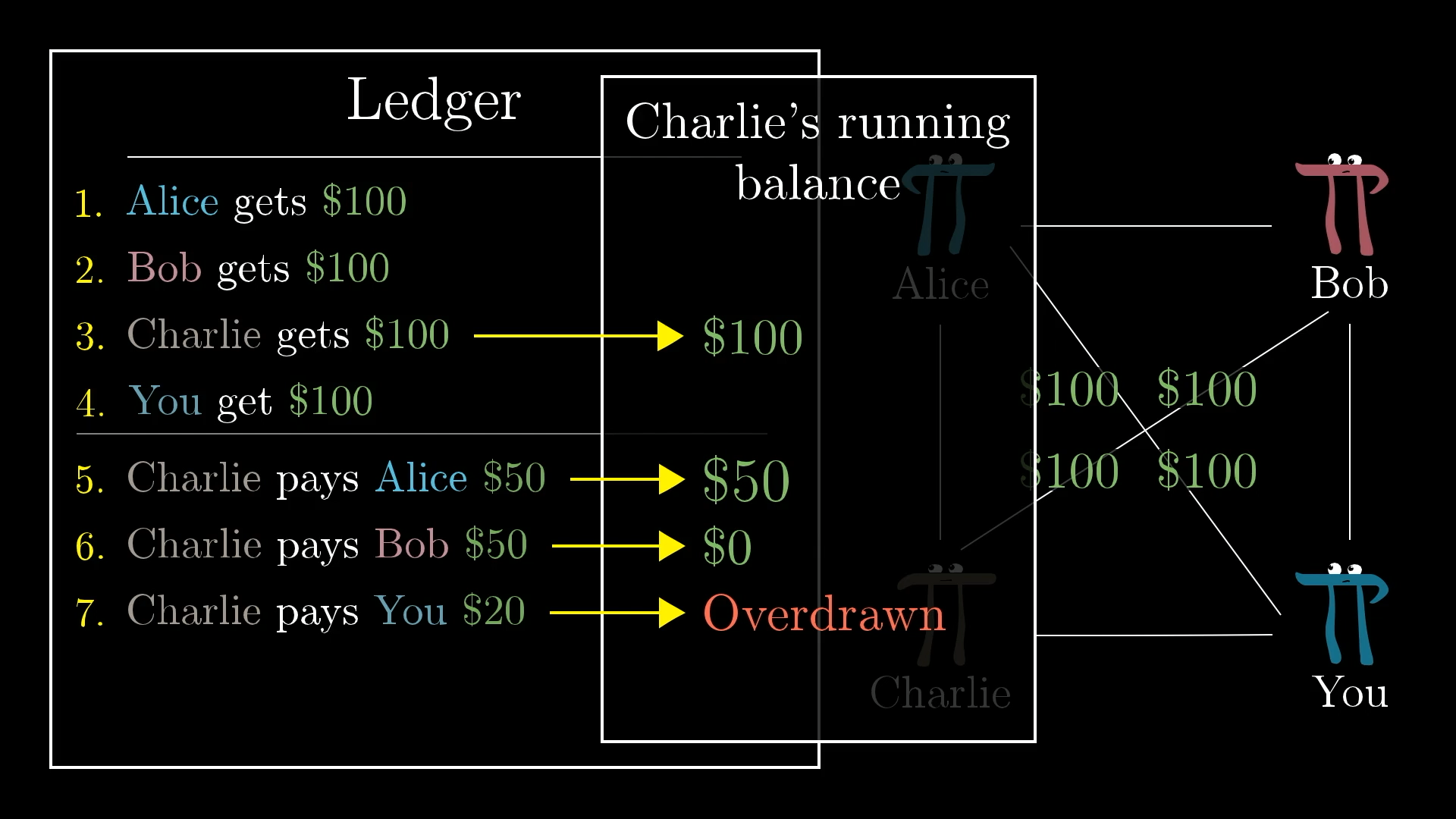
Now verifying a transaction requires checking the entire ledger history to make sure nobody overdraws.
What’s interesting here is that this step somewhat removes the connection between the Ledger and physical cash. In theory, if everyone in the world used this Ledger, you could live your whole life just sending and receiving money on this ledger without ever converting to real USD.
Who needs cash?

Actually, many of us already live our lives like this, spending and earning purely digitally while only occasionally reverting to physical cash. In that case, the relevant "ledger" is much more complicated, involving an elaborate system of banks. The big difference is that with banks we always could convert our balance on a digital account to "real" cash.
But suppose you and your friends completely detach your ledger from real cash, with no guarantee that having a positive balance there could translate into cold hard bills in your hand. To emphasize this point, let’s stop using the sign and start referring to quantities on the ledger as “Ledger Dollars” instead, or LD for short.

You are, of course, free to exchange Ledger Dollars for real US dollars. For example, maybe Alice gives Bob a $10 bill in the real world in exchange for him adding and signing the transaction “Bob pays Alice 10 LD” to the communal ledger.
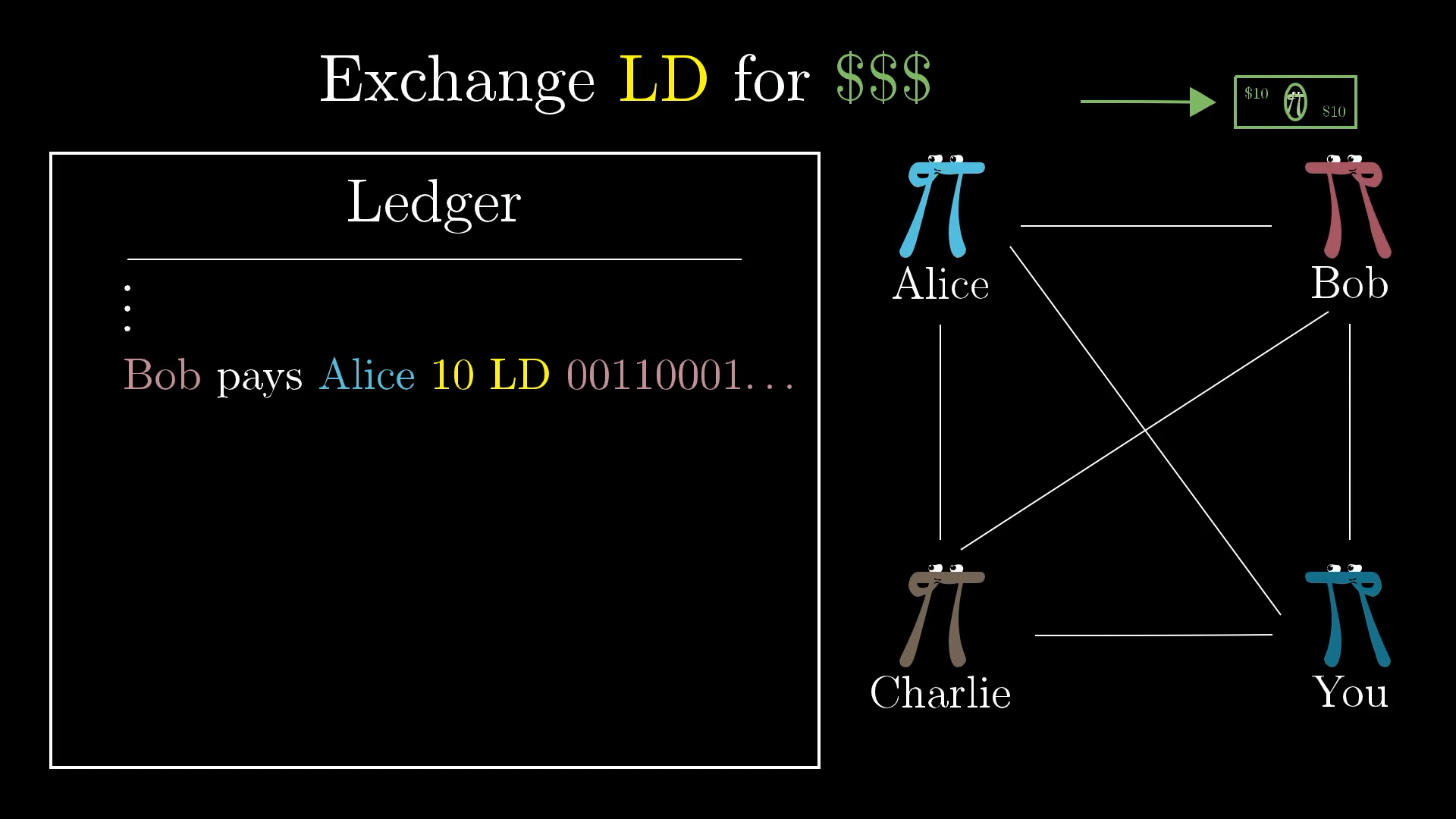
But exchanges like this are not guaranteed in the protocol. It’s now more analogous to how you might exchange Dollars for Euros or any other currency on the open market. It is its own independent thing. Also, if there's high demand to be part of ledger, it may require more than $10 of physical cash to get a transaction of 10LD pointed your way. And if there's little demand to be part of the system, it might require much less.
So our ledger is now a currency. It lacks a state to back it up, and no one is levying taxes that must be paid in Ledger Dollars, but in principle it's a closed system which allows for you and your friends to transact with each other. This brings up an important point to understand about Bitcoin, or any other cryptocurrency: Fundamentally, the cryptocurrency is just a ledger. The history of transactions is the currency.
There’s nothing else to it. No physical coin or cash. No bank or institution. To “own” a Bitcoin just means having a positive balance on the Bitcoin ledger. Or more specifically, it's to have access to the secret key associated with an entity that has a positive balance.
Of course, with Bitcoin, money doesn’t enter the Ledger with people buying in using cash. We’ll get to how new money enters the ledger in just a few minutes. But before that, there’s an even more significant difference between our current system of Ledger Dollars and how real cryptocurrencies work.
Distributing the Ledger
So far, I’ve said that this ledger is in some public place, like a website where anyone can add new lines. But this requires trusting a central location. Specifically, who hosts that website? Who controls the rules of adding new lines?

Under the current system, we need to trust the ledger owner.
To remove that bit of trust, we’ll abandon the idea of having one ledger in a central location. Instead, we’ll have everyone keep their own copy of the ledger. Then to make a transaction, like “Alice pays Bob 100 LD”, you broadcast the message into the world for people to hear and record on their own private Ledgers.
Distributing the ledger like this removes the need to trust a central authority.
But unless we do something more, this system is absurdly bad. How can you get everyone to agree on what the right ledger is? When Bob receives the transaction “Alice pays Bob 10 LD”, how can he be sure that everyone else received and believes that same transaction? If even one person doesn't know about the transaction, they might not allow Bob to spend those 10 Ledger Dollars later.

If everyone keeps a unique copy of the ledger, how can we ensure that everybody agrees on what it should say?
Really, imagine yourself just listening to transactions being broadcast. How can you be sure that everyone else is recording the same transactions you are? In those live bitcoin transactions illustrated above, how can you know if and when everyone else in the world has also heard, and will remember those as legitimate transactions in the future?
This is the real puzzle that Bitcoin solved. The novel idea Satoshi Nakamoto brought to bear in 2008 was a way to let everyone in a decentralized system agree on the validity of a single growing document, in this case a ledger, without having to trust a central source.
At a high level, the solution is to trust whichever ledger has the most computational work put into it. We’ll explain exactly what that means momentarily, but the general idea is that if you use computational work as a basis for what to trust, fraudulent transactions become computationally infeasible. That is, if you want to trick one person into trusting a ledger which is different from what the rest of the world agrees on, you'd have to have do a prohibitively large amount of work.
Again, this is getting well into the weeds beyond what anyone would need to know just to use a currency like this. But it’s a really cool idea! And if you understand it, you understand the heart of Bitcoin and other cryptocurrencies.
Hash Functions
The workhorse behind Nakamoto's solution to this puzzle is something known as a cryptographic hash function. This is a function takes in any kind of message or file as input, and outputs a string of bits with a fixed length. This output is called the “hash” or “digest” of the message, and it’s meant to look random.
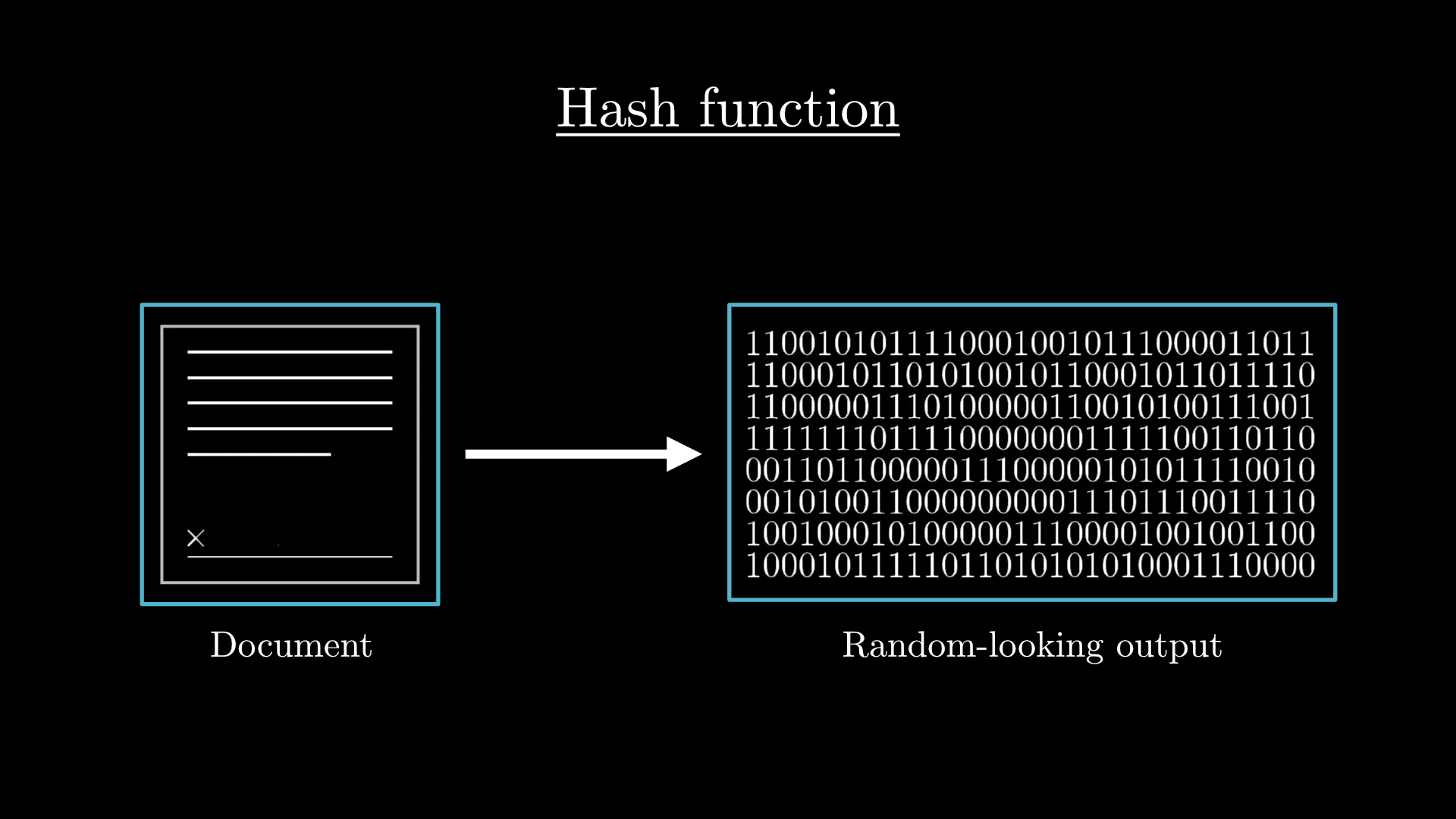
It’s not random; it always gives the same output for the same document. But the idea is that when you slightly change the input, maybe editing just one character in the document, the resulting hash changes completely.
Here’s a little playground where you can enter a message and see what its hash looks like using a special hash function known as SHA256, which is what bitcoin uses.
Notice how when you change the input text, the hash completely changes. In fact, for SHA256, the way that output changes as you slightly change the input is entirely unpredictable. This property is what makes it a cryptographic hash function.
That means it’s infeasible to compute in the reverse direction. If I show you some specific hash, like 1001111100111100...1001001110000100, and ask you to find an input message which gives that hash as output, you will have no better method than to just guess and check with random inputs.
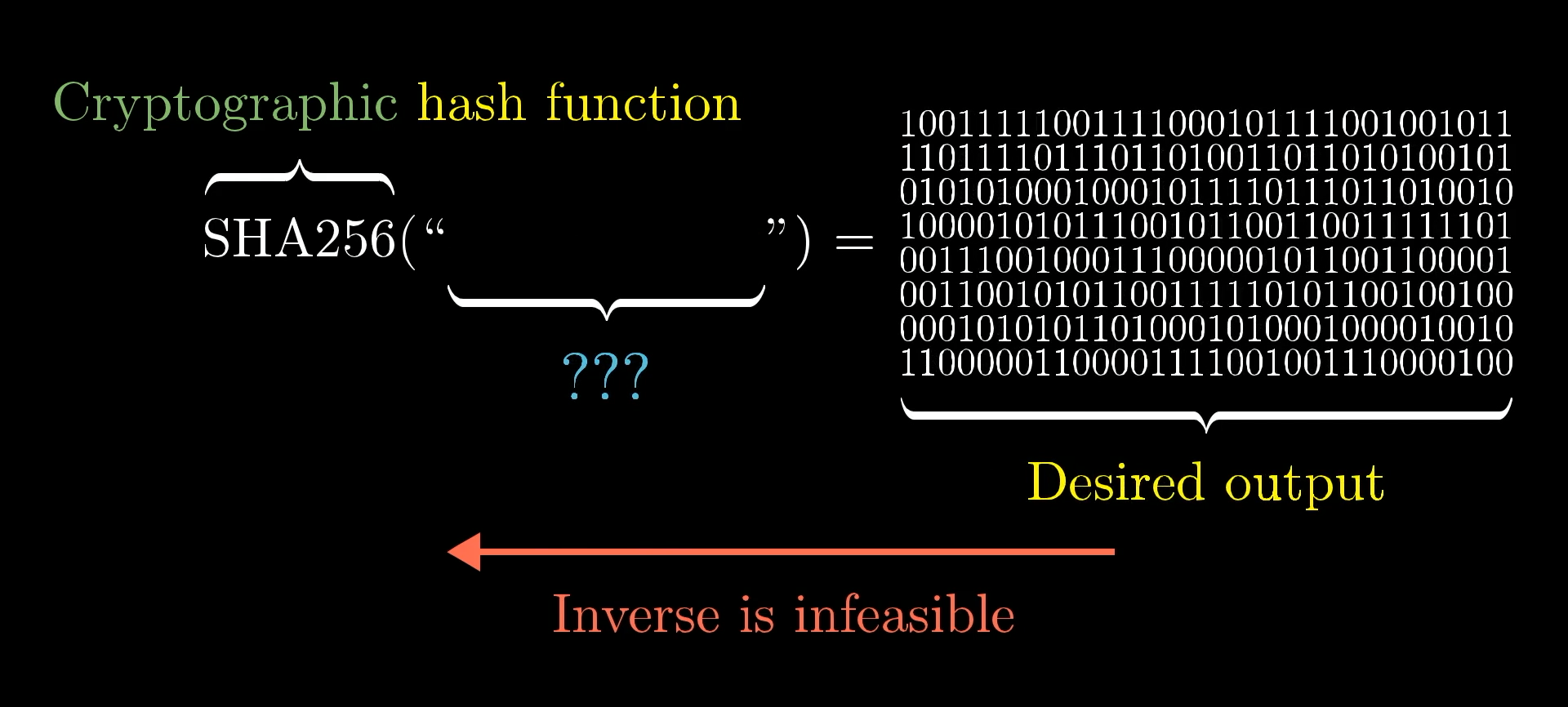
You can’t compute the inverse of the hash function (aside from just guessing and checking inputs).
Again, if you want a feel for just how much computation guesses really is, take a look at the supplement lesson. I actually had way too much fun writing that thing.
You might think you could somehow reverse engineer the desired input by really digging through the details of how the function works, but no one has ever found a way to do that.
Nobody has been able to reverse-engineer SHA256.
So how can we use this function to prove that a particular list of Bitcoin transactions is associated with a large amount of computational effort?
Proof of Work
Consider the following challenge.
In the box below I have a list of transactions, and beneath those transactions is a number. By default the number is zero, but you can change it. Everything in the box is considered one big document, and that document is being hashed using SHA256. Your goal is to change the number in the box so that the resulting hash starts with at least six zeroes.
It’s definitely possible, but it takes a while to find a solution. And, because the output of the hash function is unpredictable, there really is no better method than guessing and checking.
This challenge gets exponentially harder as the number of zeroes required increases. Finding 7 zeroes is manageable, and the largest I've found gives 9. If you find any really excellent solutions, which produce lots of zeroes, leave them in the comments!
Now suppose that someone shows you a list of transactions, and they say “I found a special number so that when you put this number at the end of the list of transactions, and apply SHA256 the entire thing, the first 30 bits of the output are all zeros”.
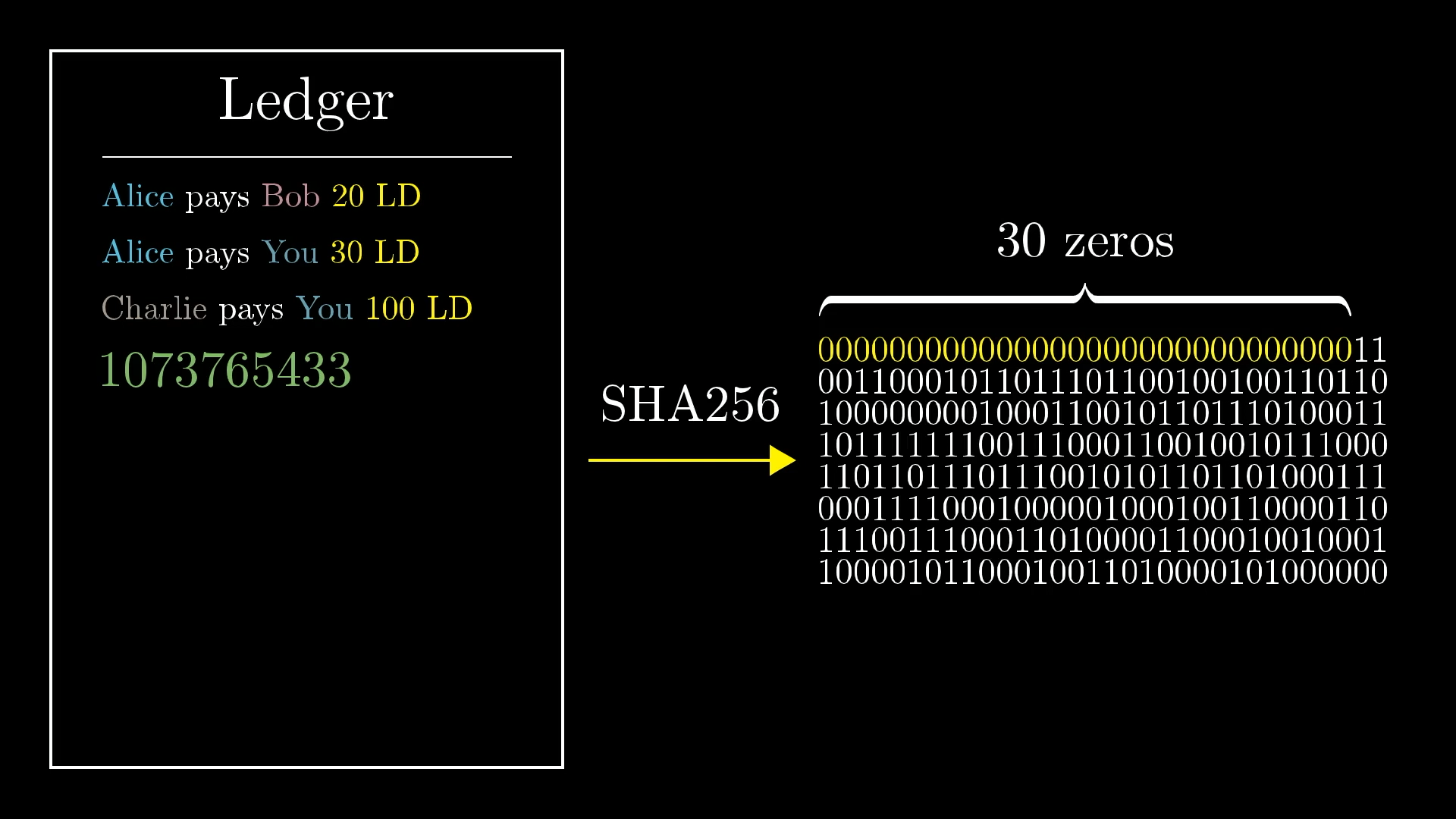
How hard do you think it was for them to find that number? The answer, of course, is that it was probably really hard.
For a random message, the probability that the hash happens to start with 30 successive zeros is in , which is about 1 in a billion. So this person almost certainly had to go through about a billion different guesses before finding this special one.
But what’s cool is that once you know the number, you can quickly verify that this hash really does start with 30 zeros. In other words, you can verify that they went through a large amount of work without having to go through that same effort yourself. This number is called a proof of work.
Importantly, all this work is intrinsically tied to that list of transactions. If you change one of the transactions, even slightly, it would completely change the hash, so you’d have to go through all that work again just to find a new number that makes the hash start with 30 zeros.
Creating a Blockchain
Think back to our distributed ledger situation. Everyone is broadcasting transactions, and we want a way for everyone to agree on what the correct ledger really is.

Everyone has their own copy of the ledger. Which one is correct?
As I said earlier, the core idea behind the original bitcoin paper is to have everybody trust whichever ledger has the most computational work put into it. So we’re going to use the many-zeroes game to prove that a ledger took a lot of work to create.
We don’t want to play the many-zeroes game by hashing the entire ledger though. What's much better is to let the work put into the ledger accumulate over time, rather than repeatedly starting over. So we start by grouping the transactions on the ledger into blocks.
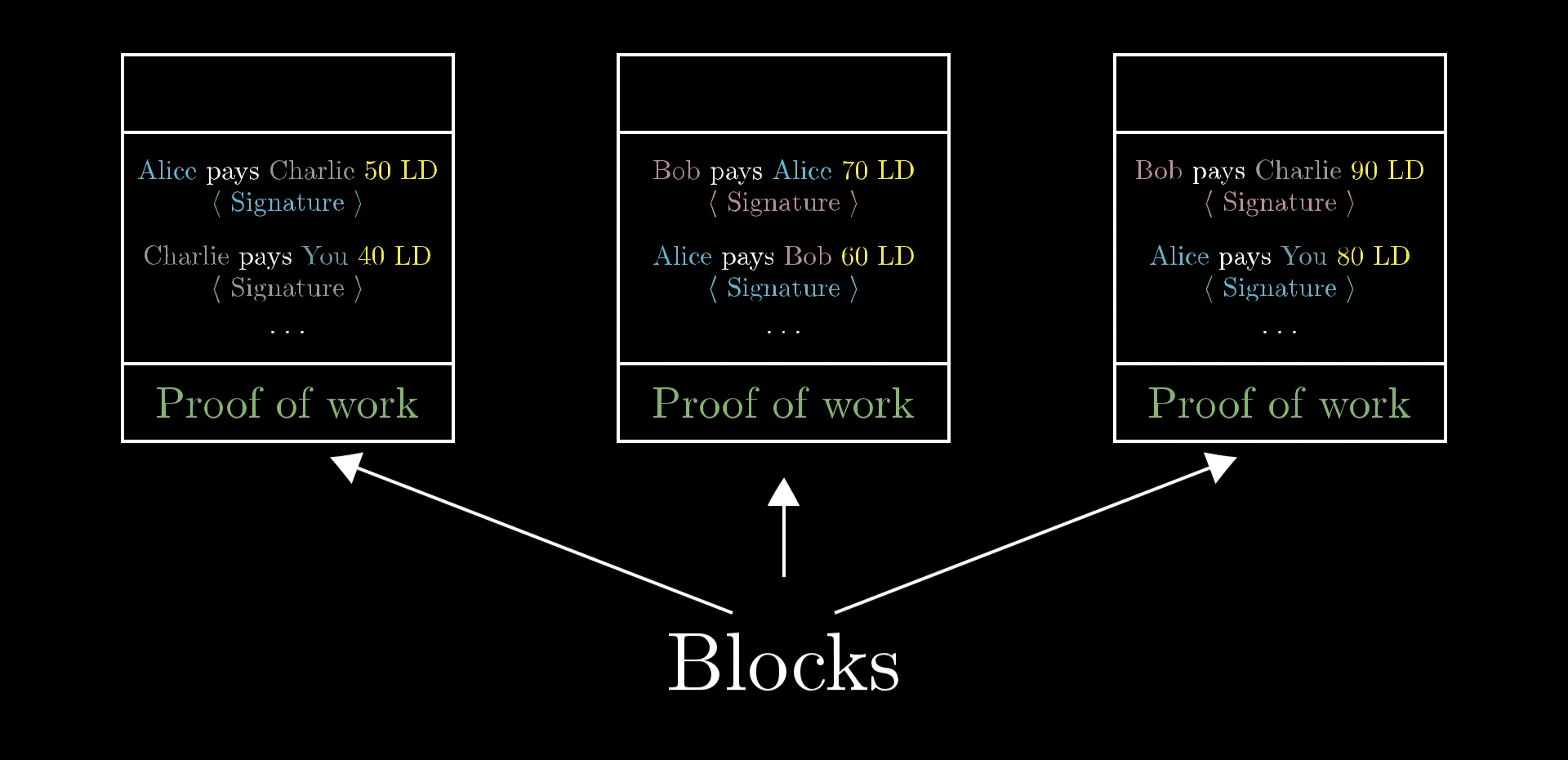
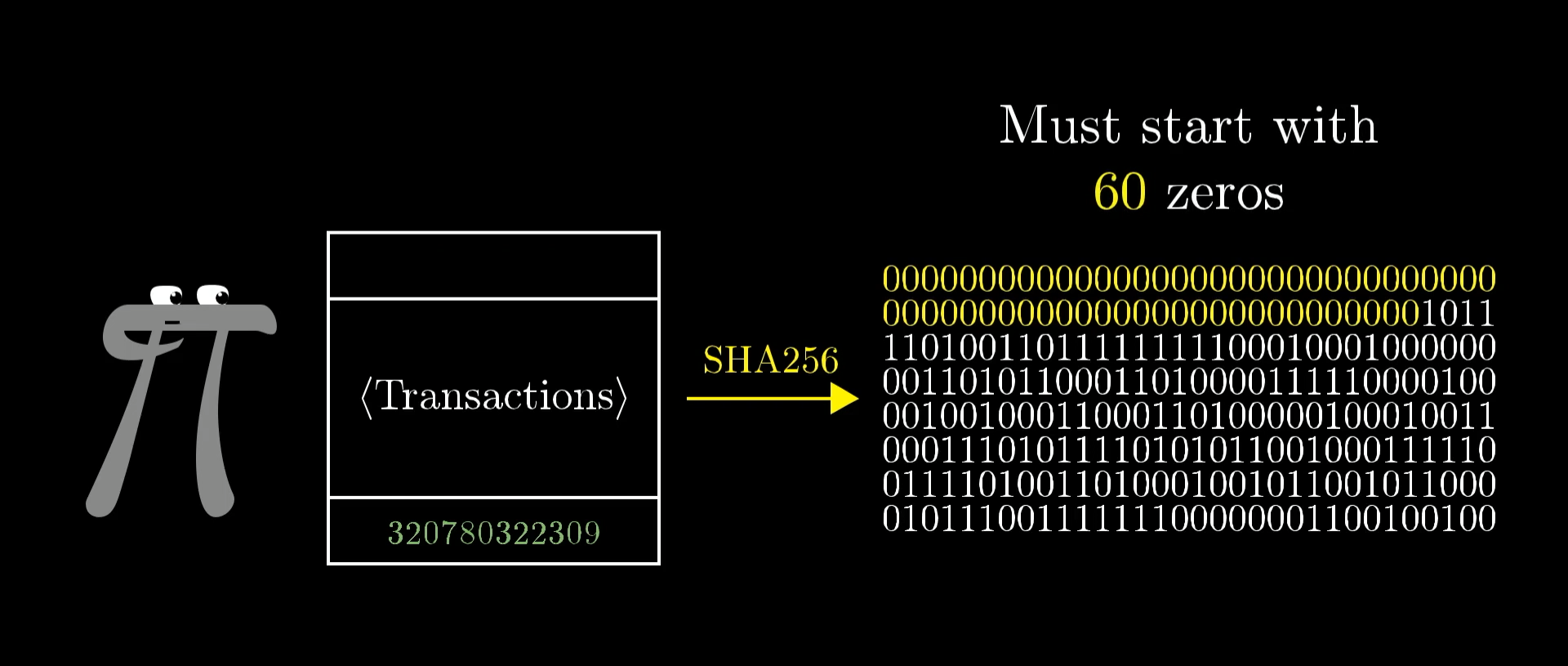
Each block consists of a list of transactions, along with a number at the bottom that is the proof of work. The proof of work must be chosen such that when you hash the entire block, the result you get starts with lots of zeroes (just like in the challenge above). For the moment let’s say it has to start with 60 zeros, but later I’ll return back to how you might choose that threshold.
In the same way that a transaction is only considered valid if it is signed by the sender, a block is only considered valid if it has a proof of work.
We also need to make sure the blocks don’t get rearranged, because that would mess with the transaction history. So we’ll say that each block must begin with the hash of the previous block. That way, the order of the blocks can’t change.
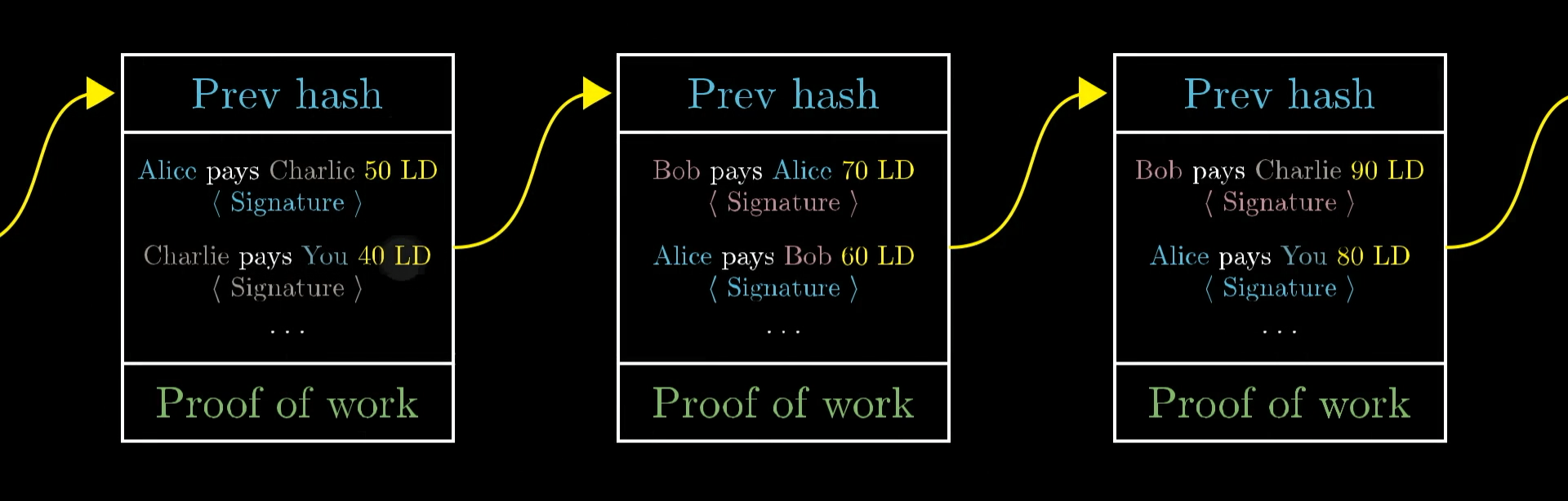
Because blocks are chained together like this, instead of calling it a ledger, this is commonly called a “blockchain”.
Block Creators (AKA “Miners”)
But now that our ledger is split into blocks, we have a bit of an issue. We can’t just add new transactions to the ledger like we used to. Instead, we’ll need a process for grouping up new transactions into blocks and computing the proof of work. So, as part of our updated protocol, we will allow anyone in the world to be a “block creator”.
What this means is that they’ll listen for the transactions being broadcast, collect them into a block, and then do a whole bunch of work to find the special number that makes the hash of this block start with 60 zeros, and broadcast out the block they found.
To reward a block creator for all this work, when they put together a block, we’ll allow them to include a special transaction at the top in which they get, say, 10 Ledger Dollars out of thin air.
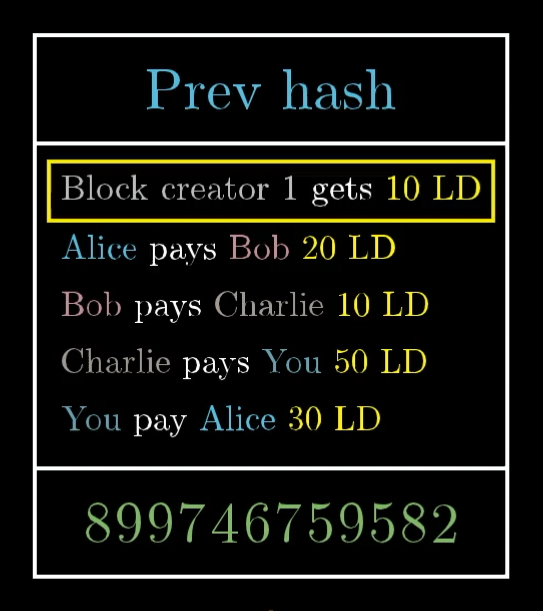
This is called the block reward. It’s a special exception to our usual rules about whether or not to accept transactions. It doesn't come from anyone, so it doesn't have to be signed. It also means that the total number of Ledger Dollars in our economy increases with each new block.
Creating blocks is often called “mining”, since it requires a lot of work, and it introduces new bits of currency into the economy. But when you hear or read about miners, keep in mind that what they’re really doing is listening to transactions, creating blocks, broadcasting those blocks, and getting rewarded with new money for doing so.
From the miner’s perspective, each block is like a miniature lottery, where everyone is guessing numbers as fast as they can until one lucky individual finds one that makes the hash of the block start with many zeros, and gets rewarded as a result.
And anyone who is just using Bitcoin (but not mining) no longer needs to listen for all the individual transactions on the network to copy them down on a personal ledger. Instead, Bitcoin users just need to keep track of the blocks that are being produced, which is much easier.
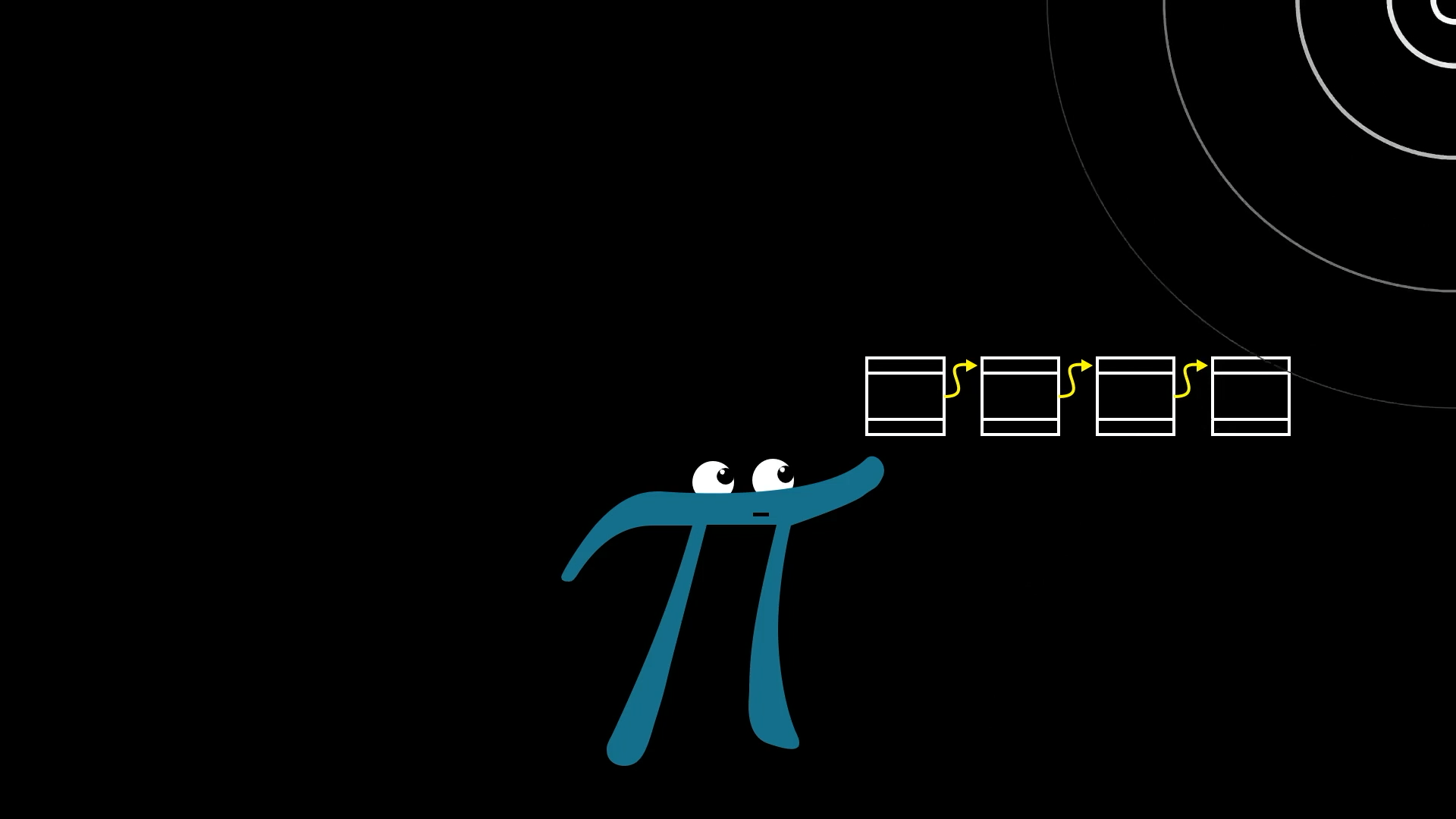
Bitcoin users just need to keep track of the blocks they’re hearing, not all the individual transactions.
The key addition is that if you hear of two miners broadcasting distinct blockchains with conflicting transaction histories, you defer to the longest one. That is, the one with the most work put into it.
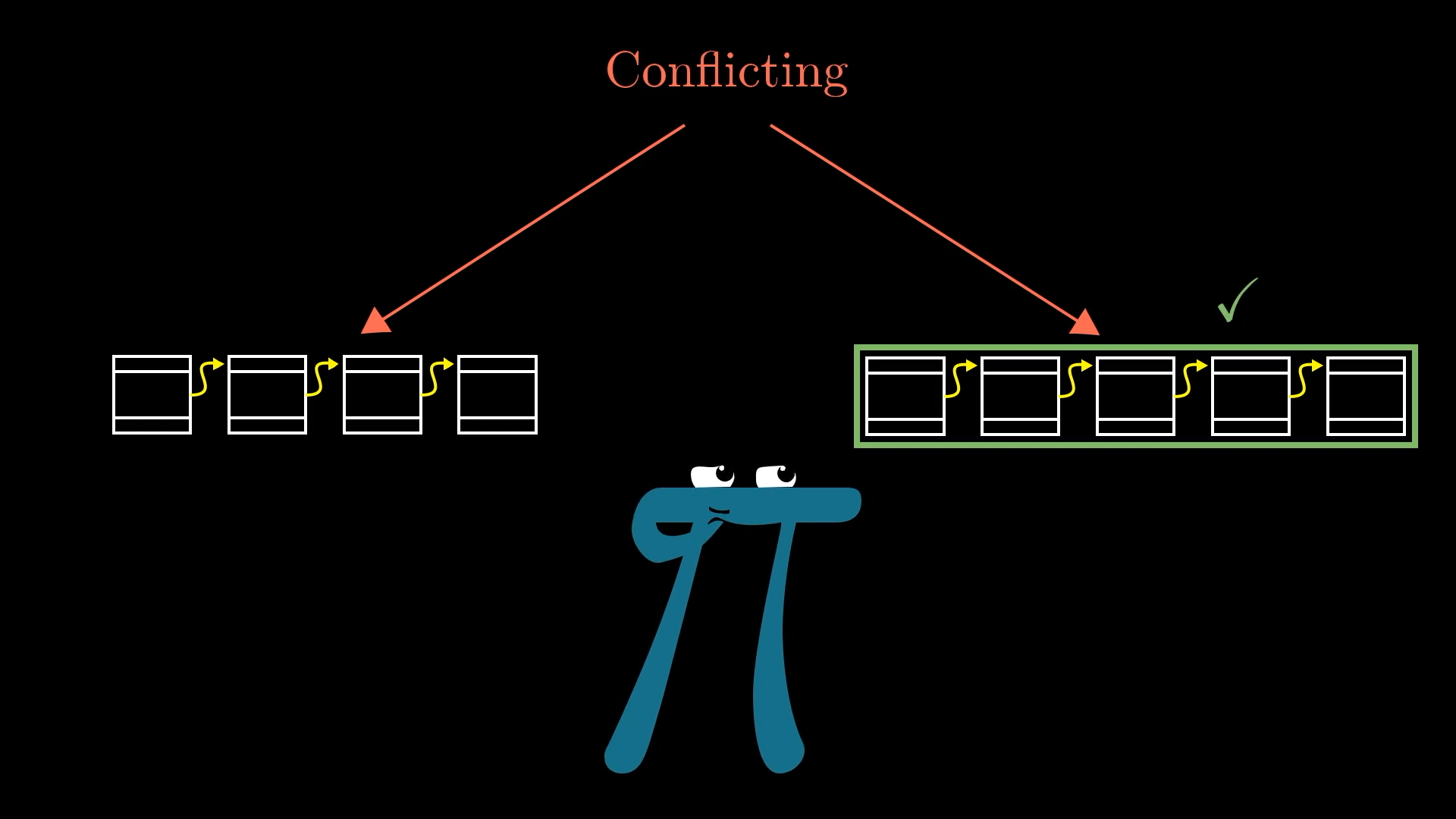
If there’s a tie, wait until you hear of an additional block that makes one longer.
So even though there is no central authority, and everyone is maintaining their own copy of the blockchain, if everyone agrees to give preference to whichever blockchain has the most work put into it, we have a way to arrive at decentralized consensus.
But out of all the systems we could use for finding consensus, why choose this one? Why always defer to the longest chain? And why are we requiring a proof of work, which artificially increases the difficulty of creating new blocks?
Alice Attempts Fraud
To see why this method is trustworthy, it’s helpful to walk through what it would take to fool someone in this system.
Suppose Alice wants to buy something from Bob for 100 LD, but without actually spending those Ledger Dollars. She might try to send him a block that includes a line saying "Alice pays Bob 100 LD", but without broadcasting that block to the rest of the network. That way Bob thinks he got paid, gives her what she bought, then later she can go back into the economy and spend those 100 LD elsewhere, and when Bob tries to spend those 100 LD other people won't treat it as valid.
To pull this off, she’d have to find a valid proof of work before all other miners that Bob is listening to, each working on their own block. And that would be difficult, but if she had a significant portion of the network's computation it could happen! Maybe Alice wins this miniature lottery before the other miners. Then she could write a block containing the fraudulent transaction and show it to Bob (but not to anyone else).
But Bob will still be hearing future broadcasts made by other miners, and Alice never told those other miners about the block she produced and gave to Bob, so they won’t include it in their own versions of the blockchain.
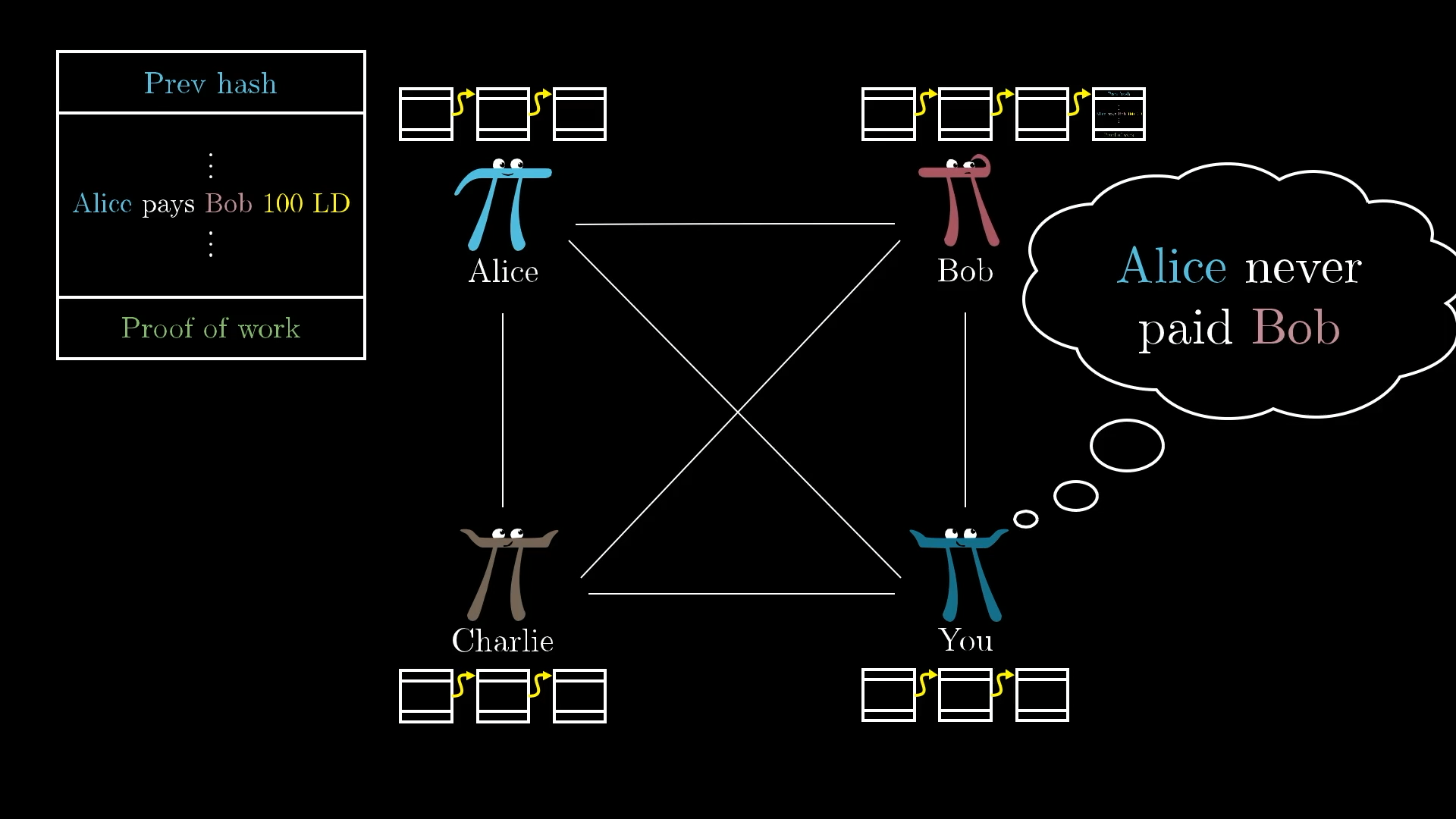
Now Bob will be hearing about conflicting chains. One from Alice, and one from everyone else. Remember, the protocol says that Bob always trusts the longest chain he knows about.
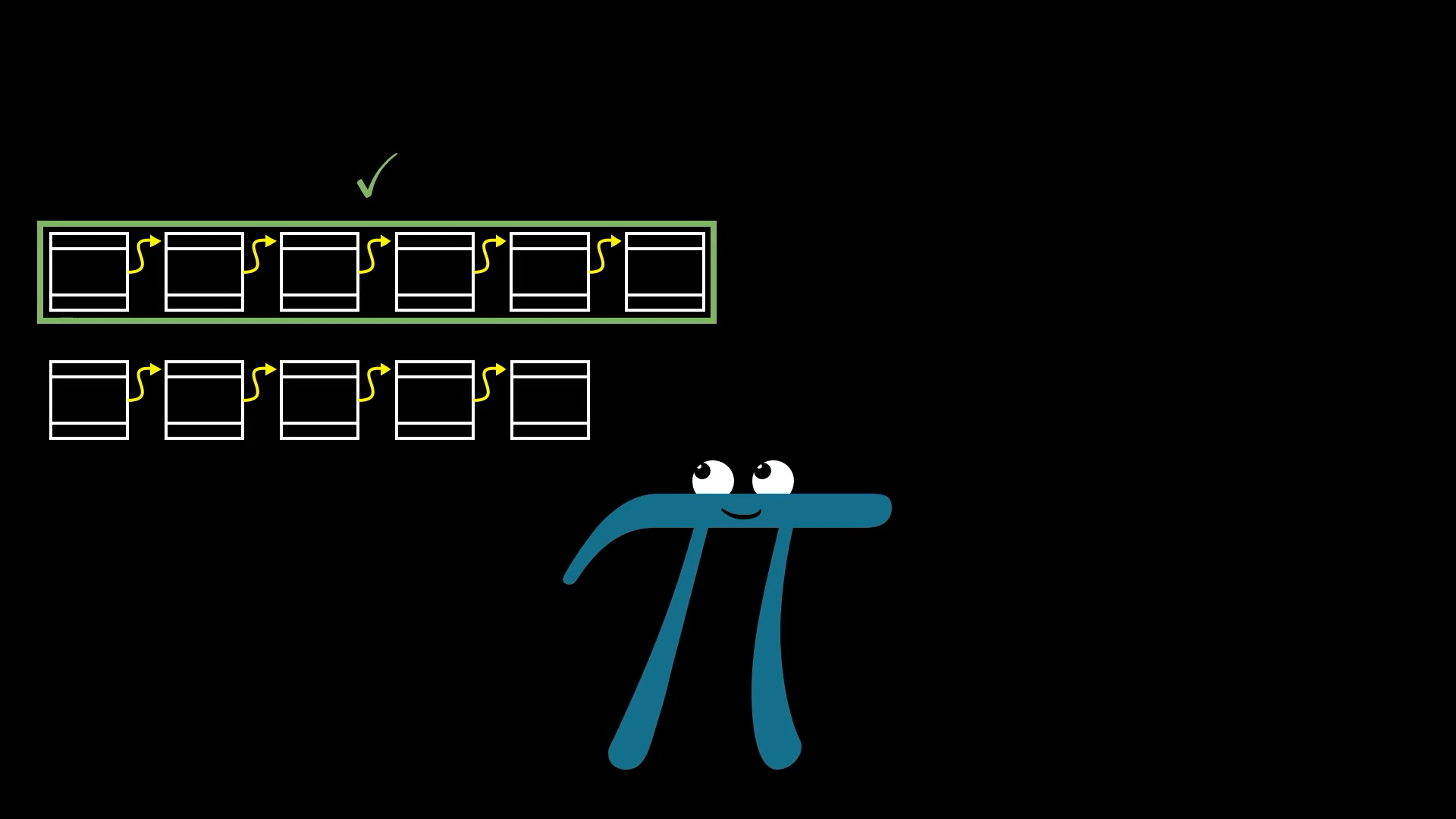
So from this point forward, Alice is in a race against all the other miners in the network to make sure her fraudulent chain always contains more blocks than the legitimate one, so that she can continue to fool Bob into thinking that her chain is the real one.
If all the other miners are able to confirm new blocks faster than Alice can, Bob will stop believing in Alice’s version, and switch to believing the other miners’ chain instead.
If Alice's computational resources are smaller than the rest of the network combined, it's more likely that the rest of the network finds a valid proof of work for their next block before she does. If she has less than 50% of the total computation on the network (and she probably has much less than that), outpacing everyone else indefinitely will be virtually impossible.
So after a while, when Alice inevitably fails to keep her chain longer, Bob will reject what he’s hearing from Alice in favor of the longer chain that everyone else is working on.
That’s what we mean when we say that the proof of work makes fraud computationally infeasible. Creating blocks is hard work, so working against the consensus is just too difficult to manage. Also, if block rewards are meaningful, it almost certainly means you're better off spending that effort mining new valid blocks than trying to fool one individual.
It’s worth noting that building a single fraudulent block is definitely possible. The difficulty is in maintaining the lie for a long time. So to avoid being tricked, a user shouldn't necessarily trust a new block that they hear immediately. Instead, they should wait for several new blocks to be added on top of it. If they still haven’t heard of any longer blockchains, they can trust that this block is part of the same chain everyone else is using.
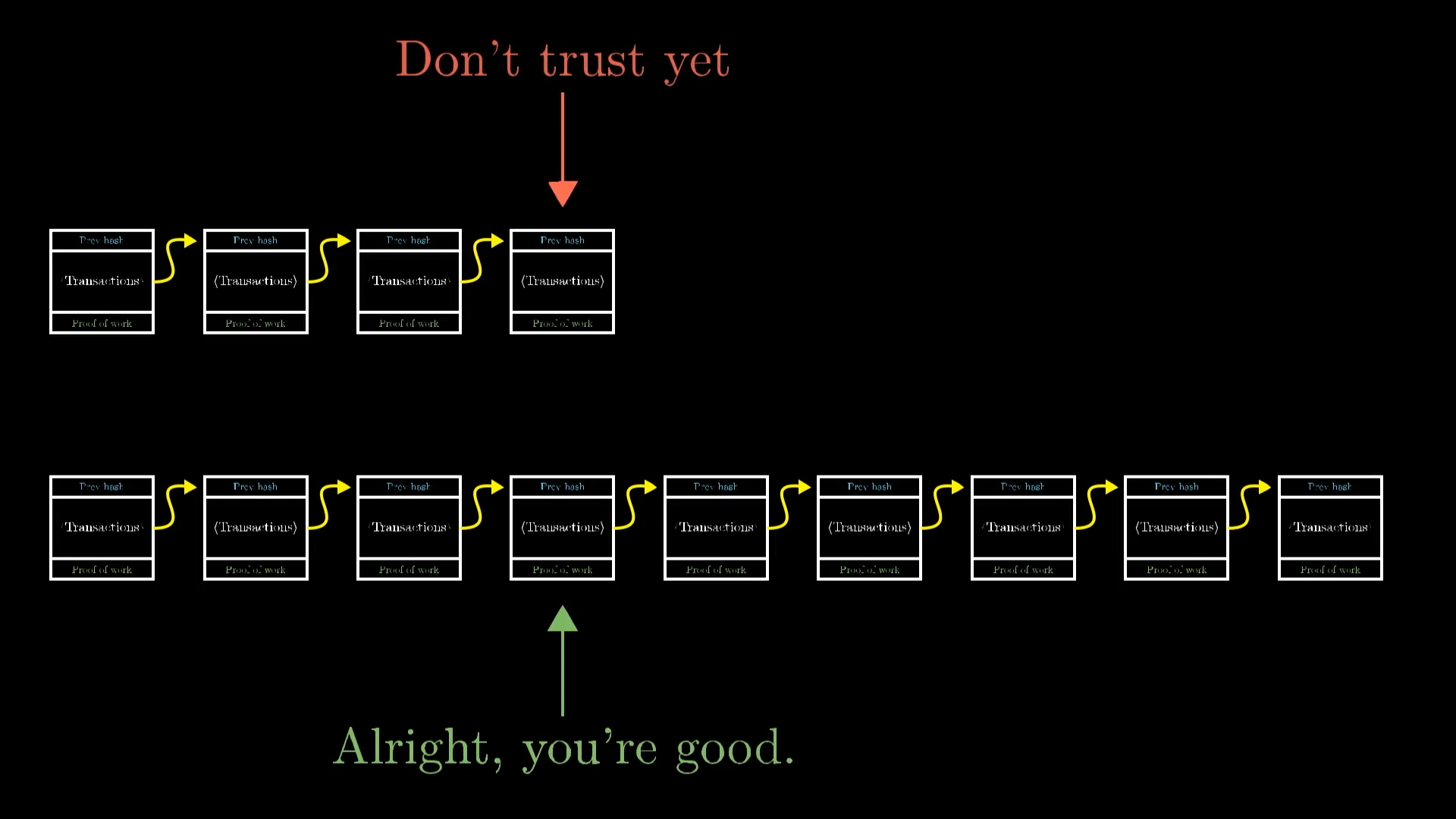
Blocks are most trustworthy when they aren’t brand new.
Ledger Dollars vs. Bitcoin
With that, we’ve hit all the main ideas. This distributed ledger system based on a proof of work is more or less how the Bitcoin protocol works, and how many other cryptocurrencies work. There’s just a few details to clear up.
Earlier I said that the proof of work challenge might be to find a special number so that the hash of the block starts with 60 zeros. The way the actual bitcoin protocol works is to systematically change that number of zeros so that it always takes the world about 10 minutes to find a new block. So, as there are more and more miners on the network, the challenge gets harder and harder in such a way that this miniature lottery only has about one winner every 10 minutes.
Also, all of the money in Bitcoin ultimately comes from some block reward. Nobody “buys in” to Bitcoin like we originally said while building up our own Ledger Dollars. When Bitcoin first got started, the reward was 50 Bitcoin per block. There’s a great site called Block Explorer where you can look through the Bitcoin blockchain. If you look at the very first few blocks on the chain, they contain no transactions other than the 50 Bitcoin reward to the miner. Every 210,000 blocks, which is about every 4 years, that reward gets cut in half. So right now, as of 2021, the reward is at 6.25 Bitcoin per block, and because this reward decreases geometrically over time, there will never be more than 21 million bitcoin in existence.
However, this doesn't mean miners will stop earning money. In addition to the block reward, miners can also pick up transaction fees. The way this works is that whenever you make a payment, you can optionally include a small transaction fee with it that will go to the miner of whatever block includes that payment.

The reason you might do this is to incentivize miners to actually include your transaction in the next block. It’s up to the miners to decide which transactions they want to include on the block they are computing hashes for, so it makes sense to incentivize them to include yours.
You see, in Bitcoin, each block is limited to about 2,400 transactions, which many critics argue is unnecessarily restrictive.
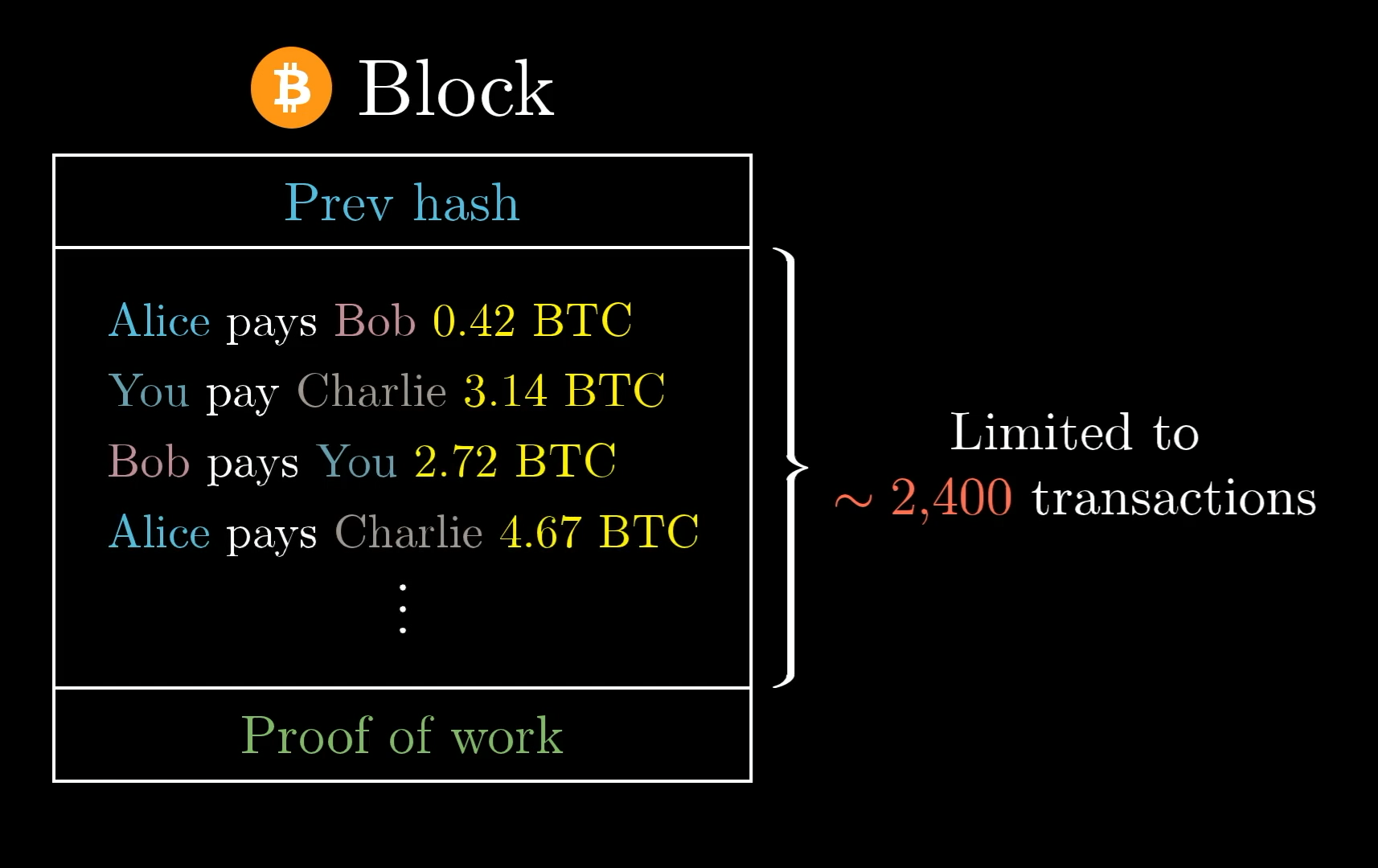
Since Bitcoin aims to add about one block every 10 minutes, only about 4 Bitcoin transactions can be processed per second (give or take). For comparison, Visa processes an average of around 1,700 transactions per second, and they’re capable of handling more than 24,000 per second. Slower processing on Bitcoin means higher transaction fees, since that’s what determines which transactions miners choose to include in new blocks.
In addition to being slow, Bitcoin is also criticized for using too much energy. The proof-of-work idea is a clever way to prevent fraud, but it means that mining blocks requires a truly insane amount of resources.
According to the Cambridge Bitcoin Electricity Consumption Index, Bitcoin mining currently (as of 2021) uses about 115 Terrawatt-Hours of electricity per year. To put that in perspective, it's substantially more than the entire country of Finland uses.
Since 2008, one alternative to proof work has cropped up known as "proof of stake", which uses dramatically less energy, and which several newer cryptocurrencies have started to use.
Conclusion
This is far from a comprehensive coverage of cryptocurrencies. There are many nuances and alternate design choices I haven’t touched here, but the goal is to provide a stable Wait-but-Why-style tree trunk of understanding for anyone looking to add a few more branches with further reading.
I originally made the video underlying this lesson in 2017, in the midst of a new wave of attention and money flowing toward cryptocurrencies, although at that time I didn't realize how much more there was to come. It was a bit disappointing to see the onslaught of spam and scams that made its way into the comments of that video, though perhaps that's inevitable for a topic so tied to money.
Even if the monetary aspect of it is what draws in people's attention (after all, why else would so many suddenly want to learn about cryptography?), the hope here is that your takeaway is an appreciation for the cleverness and usefulness of objects like digital signatures and cryptographic hash functions. And more then that, the hope is that you appreciate how powerful it is to be able to construct functions with the properties these claim to have, as it's an example of some surprisingly sophisticated math making its way into widespread use.
Thanks
Special thanks to those below for supporting the original video behind this post, and to current patrons for funding ongoing projects. If you find these lessons valuable, consider joining.