e^(iπ) in 3.14 minutes, using dynamics
A quick explanation of e^(pi i) in terms of motion and differential equations
The Real Case
One way to think about the function e^t is to ask what properties it has. Probably the most important one, from some points of view the defining property, is that it's a function which is equal to its own derivative. Together with the added condition that inputting 0 returns 1, it's the only function with this property.
You can illustrate what that means with a physical model: Think of e^t as your position on a number line as a function of time. The condition e^0 = 1 means you start at 1. The equation above is saying that your velocity, the derivative of position, is always equal to your position. In other words, the farther away from 0 you are, the faster you move, with the very specific constraint that your velocity vector is perpetually identical to your position vector.
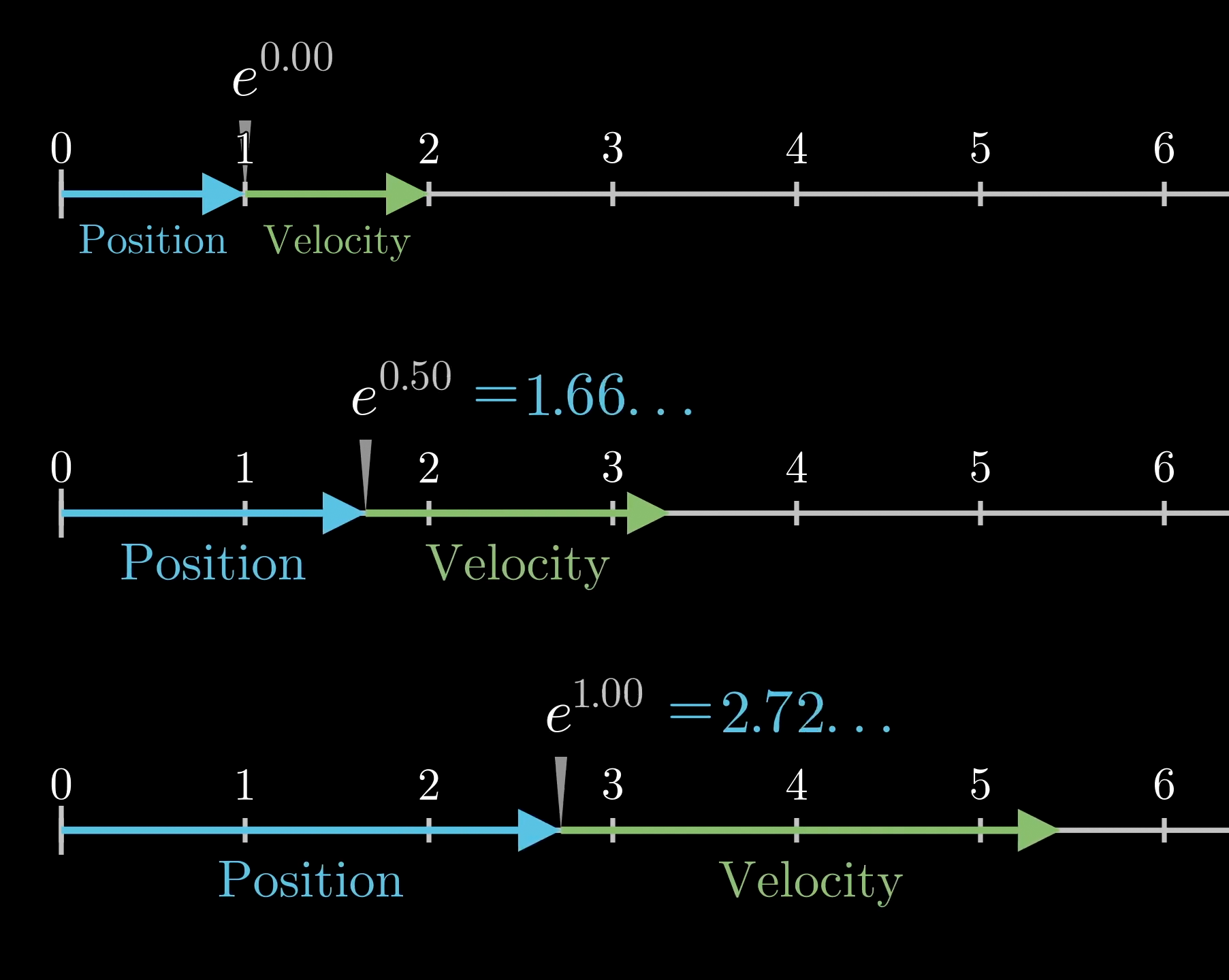
So even before knowing how to compute e^t exactly, this ability to associate each position with the velocity you must have at that position paints a very strong intuitive picture of how the function must grow. You know you'll be accelerating, at an accelerating rate, with an all-around feeling of things getting out of hand quickly.
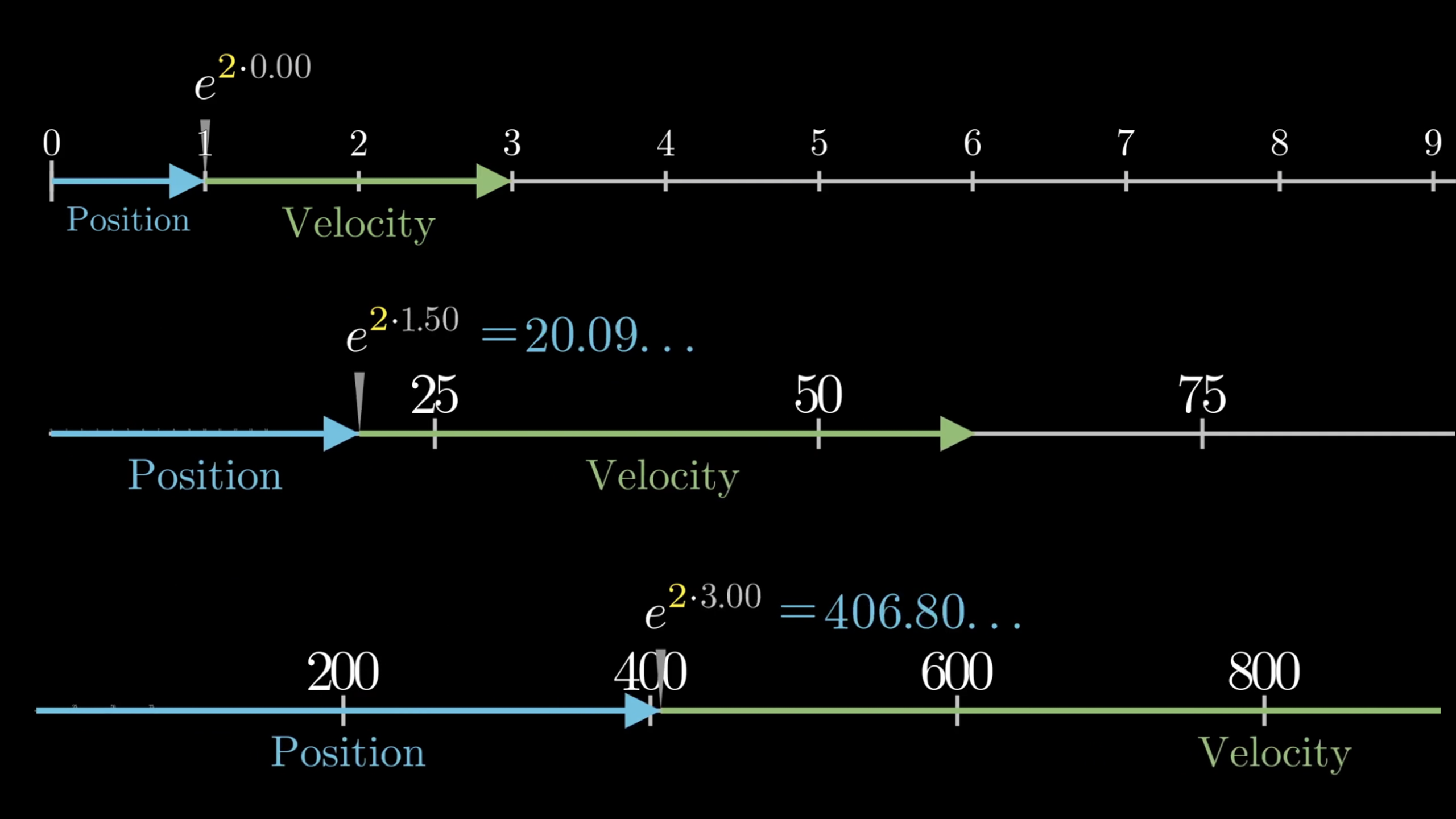
If we add a constant to this exponent, like e^{2t}, the chain rule tells us the derivative of our function is now 2 times the function itself.
So at every point on the number line, rather than attaching a vector corresponding to the number itself, first double the magnitude, then attach it. Moving so that your position is always e^{2t} is the same thing as moving in such a way that your velocity is always twice your position. The implication of that 2 is that our runaway growth feels all the more out of control.
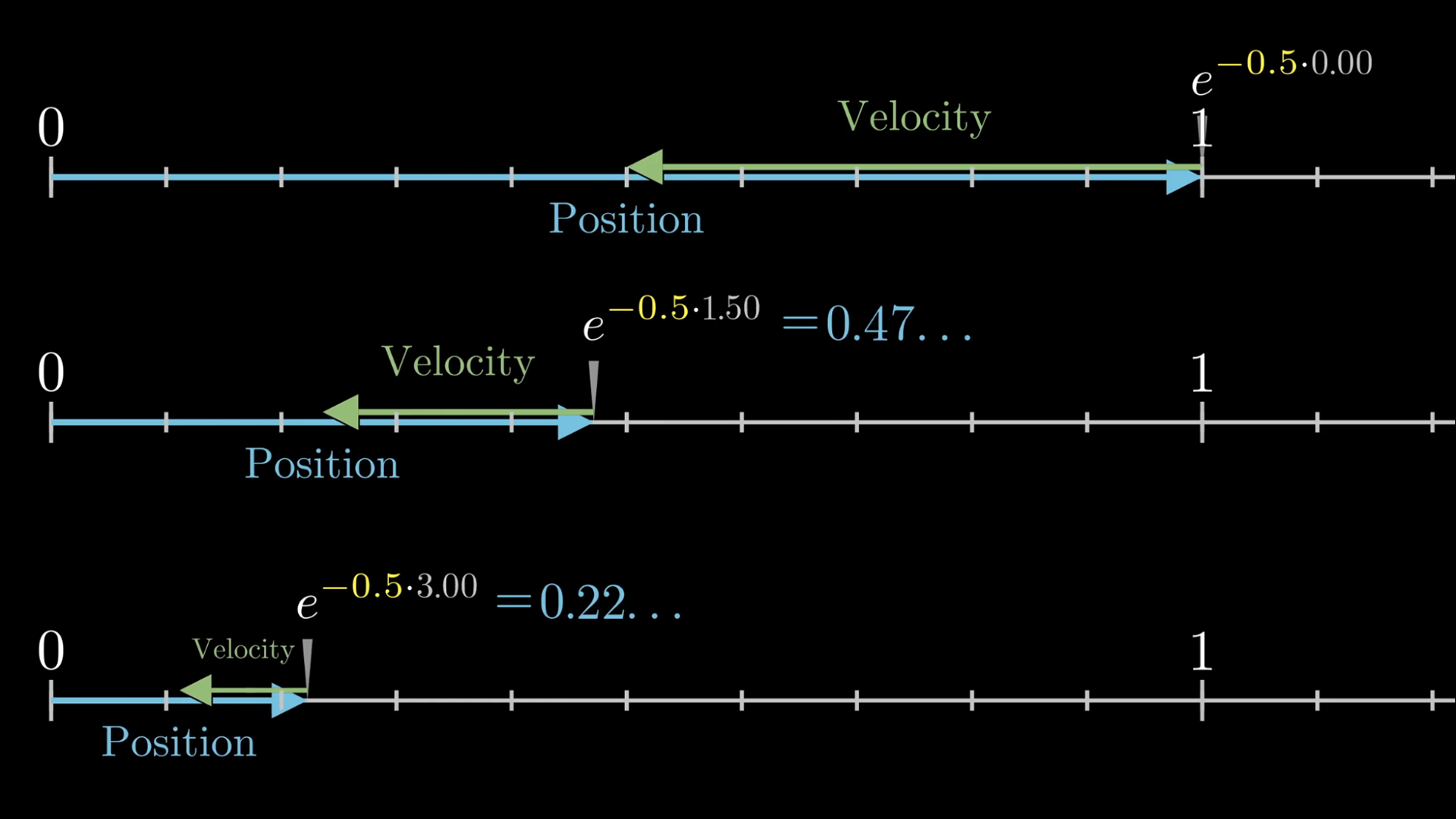
If that constant was negative, say -0.5, then your velocity vector is always -0.5 times your position vector, meaning you flip it around 180-degrees, and scale its length by a half.
Moving in such a way that your velocity always matches this flipped and squished copy of the position vector, you'd go the other direction, slowing down in exponential decay towards 0.
The complex case
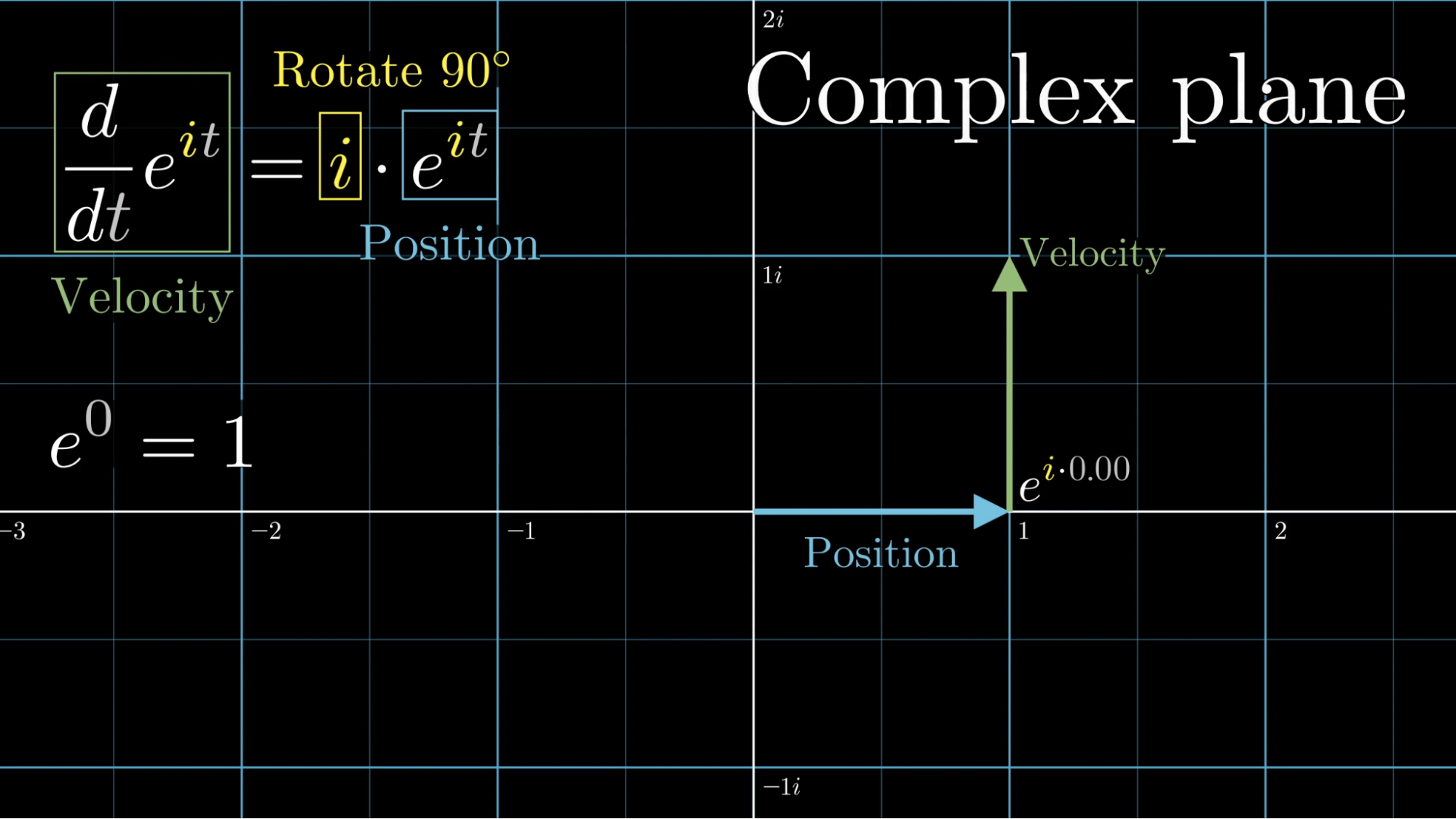
What about if the constant was i, the imaginary unit? If your position was always e^{it}, how would you move as that time, t, ticks forward?
Well, assuming there's any way to make sense out of e^{it}, and assuming that derivatives still work the way we'd expect when extending to complex numbers, the derivative of your position e^{it} would now always be i times itself. Multiplying by i has the effect of rotating numbers 90-degrees, and as you might expect, things only make sense here if we start thinking beyond the number line and in the complex plane.
So what does e^{it} mean?
So even before you know how to compute e^{it}, you know that for any position this might give for some value of t, the velocity at that time will be a 90-degree rotation of that position.
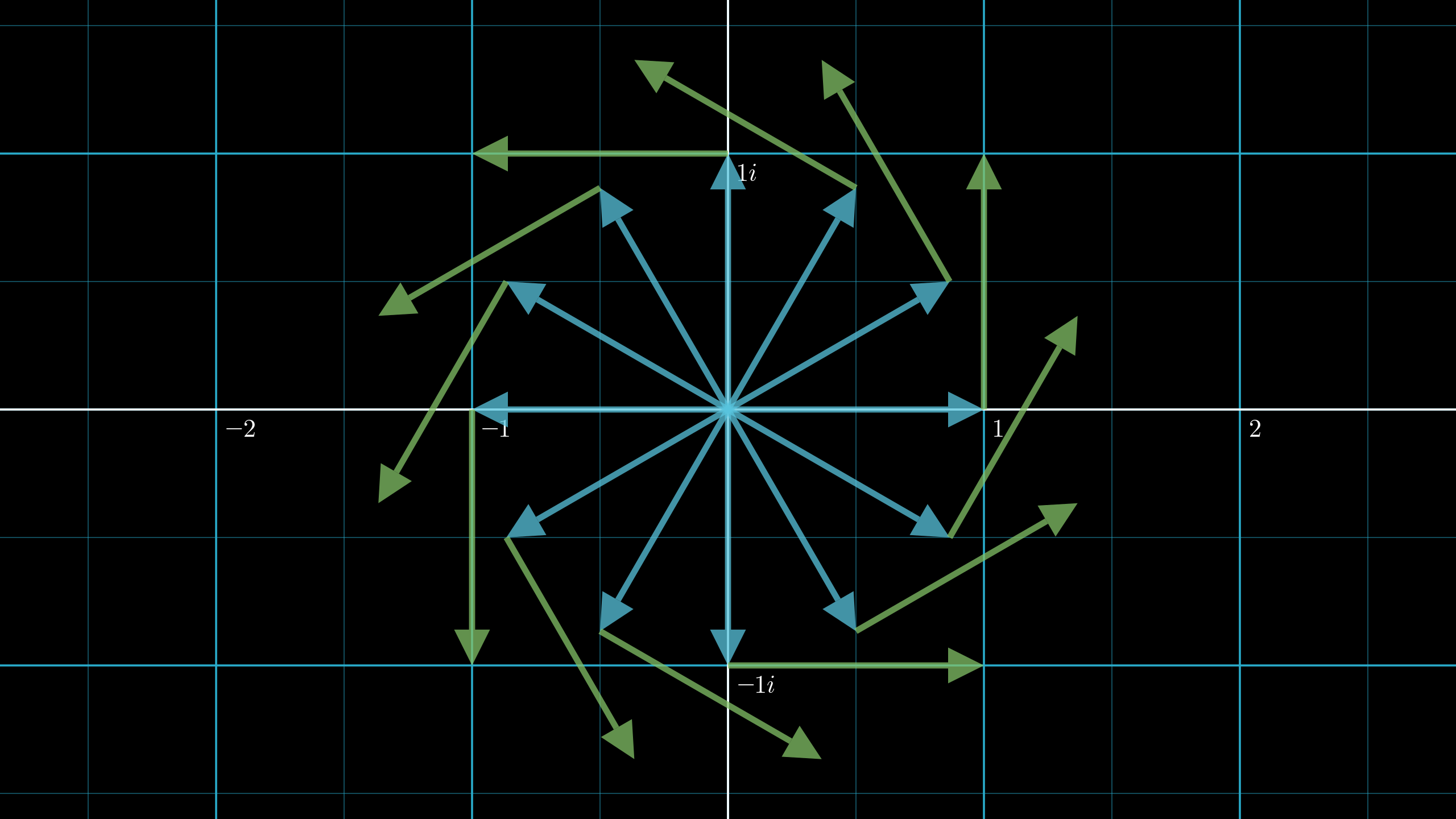
Each blue arrow above pointing outward from the origin represents an example
value of e^{it}, thought of as a position vector. The corresponding green
arrow at its tip shows what the velocity, equal to the position rotated 90
degrees counterclockwise, would have to be for that particular position.
Drawing this for all possible positions you might come across, we get a vector field, where, usually with vector fields we shrink things down to avoid clutter.
At time t=0, e^{it} will be 1. There's only one trajectory starting from that position where your velocity is always matching the vector it's passing through, a 90-degree rotation of position. It's when you go around the unit circle at a speed of 1 unit per second.
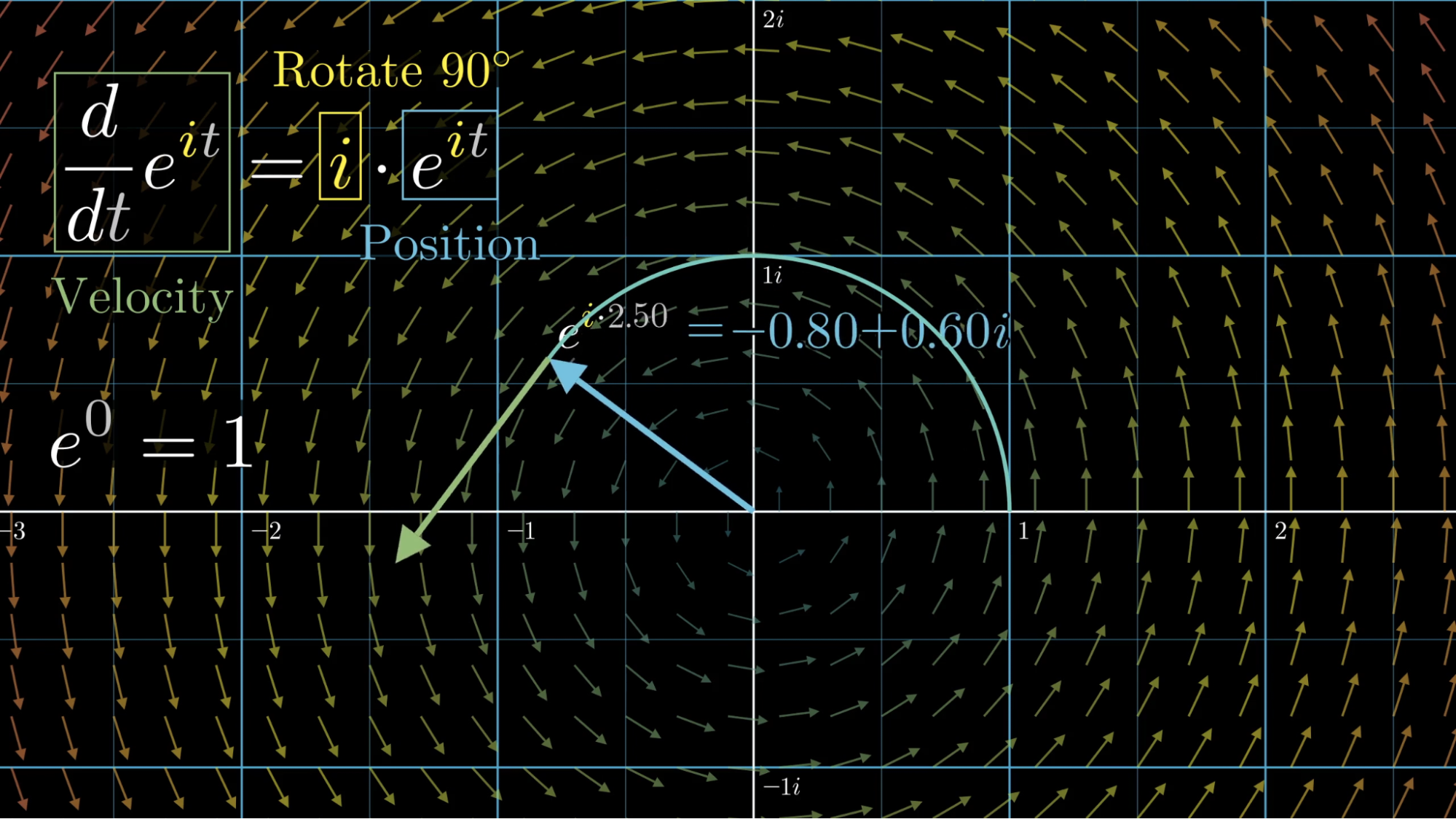
So after \pi seconds, you've traced a distance of \pi around; e^{i\pi} = -1.
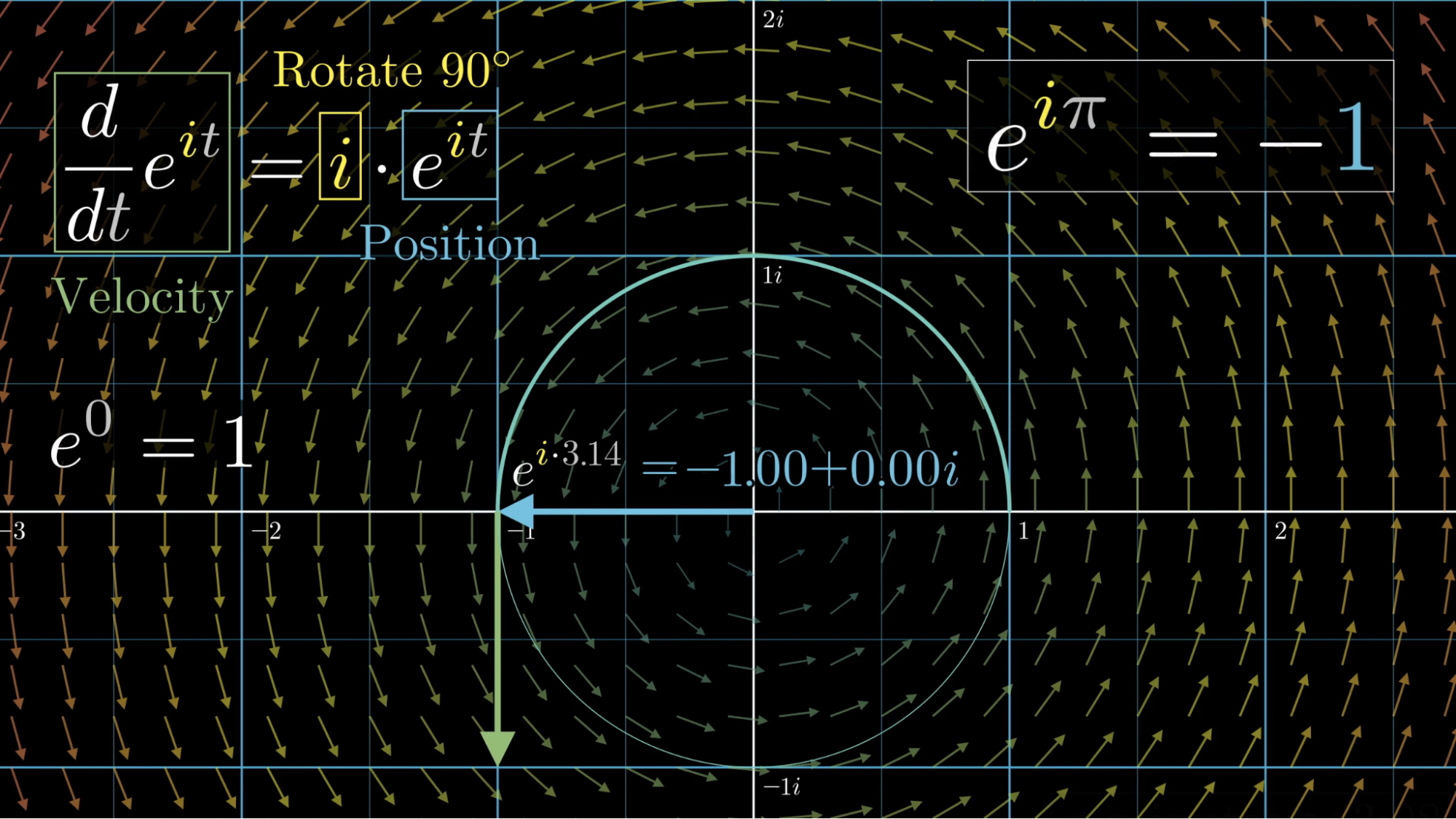
After \tau = 2\pi seconds, you've gone full circle; e^{i\tau} = 1.
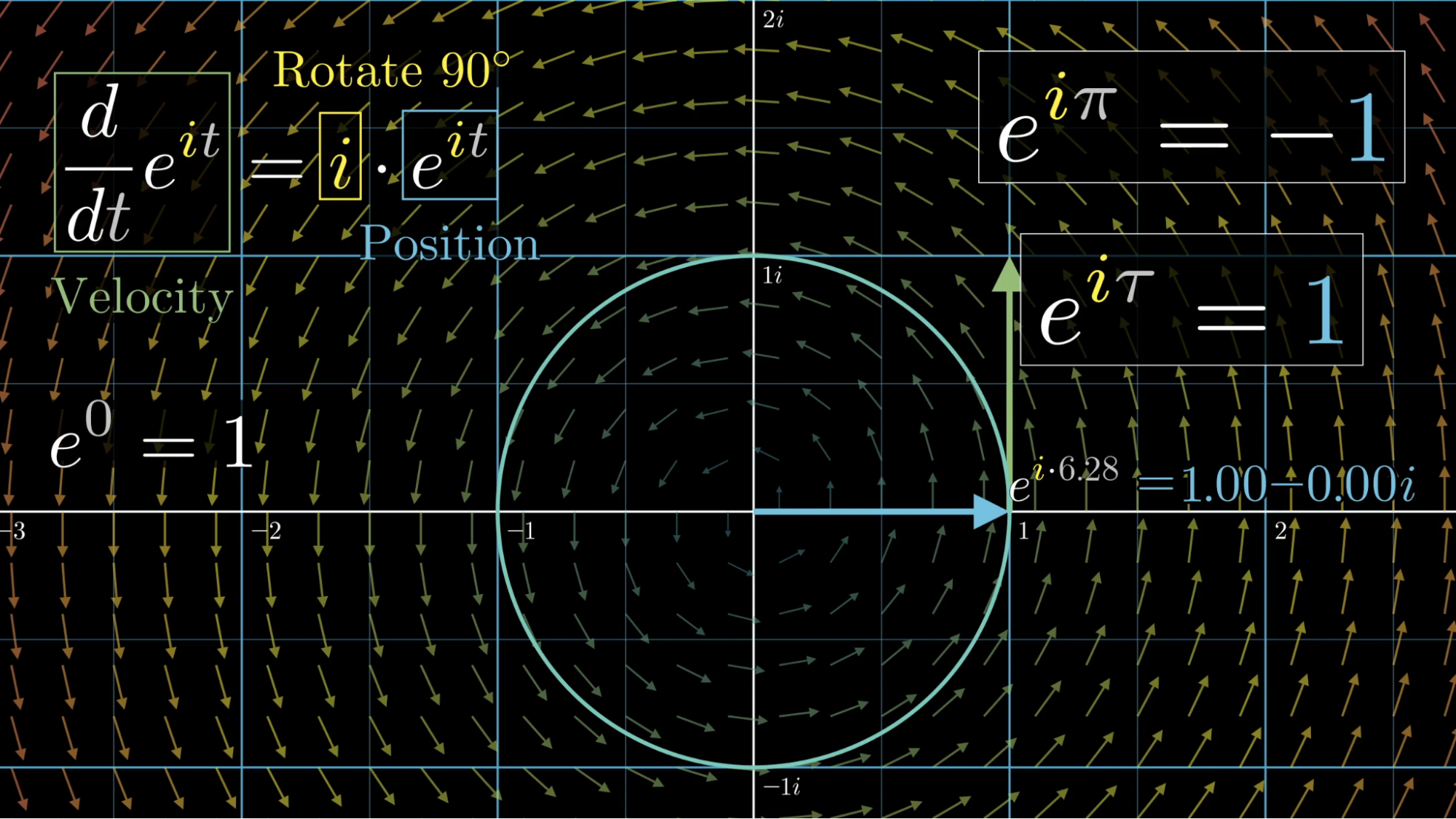
And more generally, e^{it} equals a number t radians around this circle.
Nevertheless, something might still feel immoral about putting an imaginary number up in that exponent. And you'd be right to question that! For values of x which are not real numbers, what we write as e^x has very little to do with repeated multiplication, and its relation to the number e feels frankly more incidental than definitional. To dig in a little bit deeper, the covers more general exponents, with a focus on matrices.
