Chapter 3Linear transformations and matrices

"Unfortunately, no one can be told what the Matrix is. You have to see it for yourself."

- Morpheus

If there was one topic that makes all of the others in linear algebra start to click, it might be this one. We'll be learning about the idea of a linear transformation, and its relation to matrices. For this chapter, the focus will simply be on what these linear transformations look like in the case of two-dimensions, and how they relate to the idea of matrix-vector multiplication. In particular, we want to show you a way to think about matrix multiplication that doesn't rely on memorization.

Transformations Are Functions

To start, let's parse this term: "Linear transformation". Transformation is essentially a fancy word for function; it's something that takes in inputs, and spit out some output for each one. Specifically, in the context of linear algebra, we think about transformations that take in some vector, and spit out another vector.

So why use the word "transformation" instead of "function" if they mean the same thing? It's to be suggestive of a certain way to visualize this input-output relation. Rather than trying to use something like a graph, which really only works in the case of functions that take in one or two numbers and output a number, a great way to understand functions of vectors is to use movement.

'Transformation' suggests movement!

If a transformation takes some input vector to some output vector, we imagine that input vector moving to the output vector.

StillAnimation

To understand the transformation as a whole, we imagine every possible vector move to its corresponding output vector.

StillAnimation

It gets very crowded to think about all vectors all at once, each as an arrow. So let's think of each vector not as an arrow, but as a single point: the point where its tip sits. That way, to think about a transformation taking every possible input vector to its corresponding output vector, we watch every point in space move to some other point.

StillAnimation

In the case of transformations in two dimensions, to get a better feel for the shape of a transformation, we can do this with all the points on an infinite grid. It can also be helpful to keep a static copy of the grid in the background, just to help keep track of where everything ends up relative to where it starts.

Visualizing functions with 2d inputs and 2d outputs like this can be beautiful, and it's often difficult to communicate the idea on a static medium like a blackboard. Here are couple more particularly pretty examples of such functions.

StillAnimation

StillAnimation

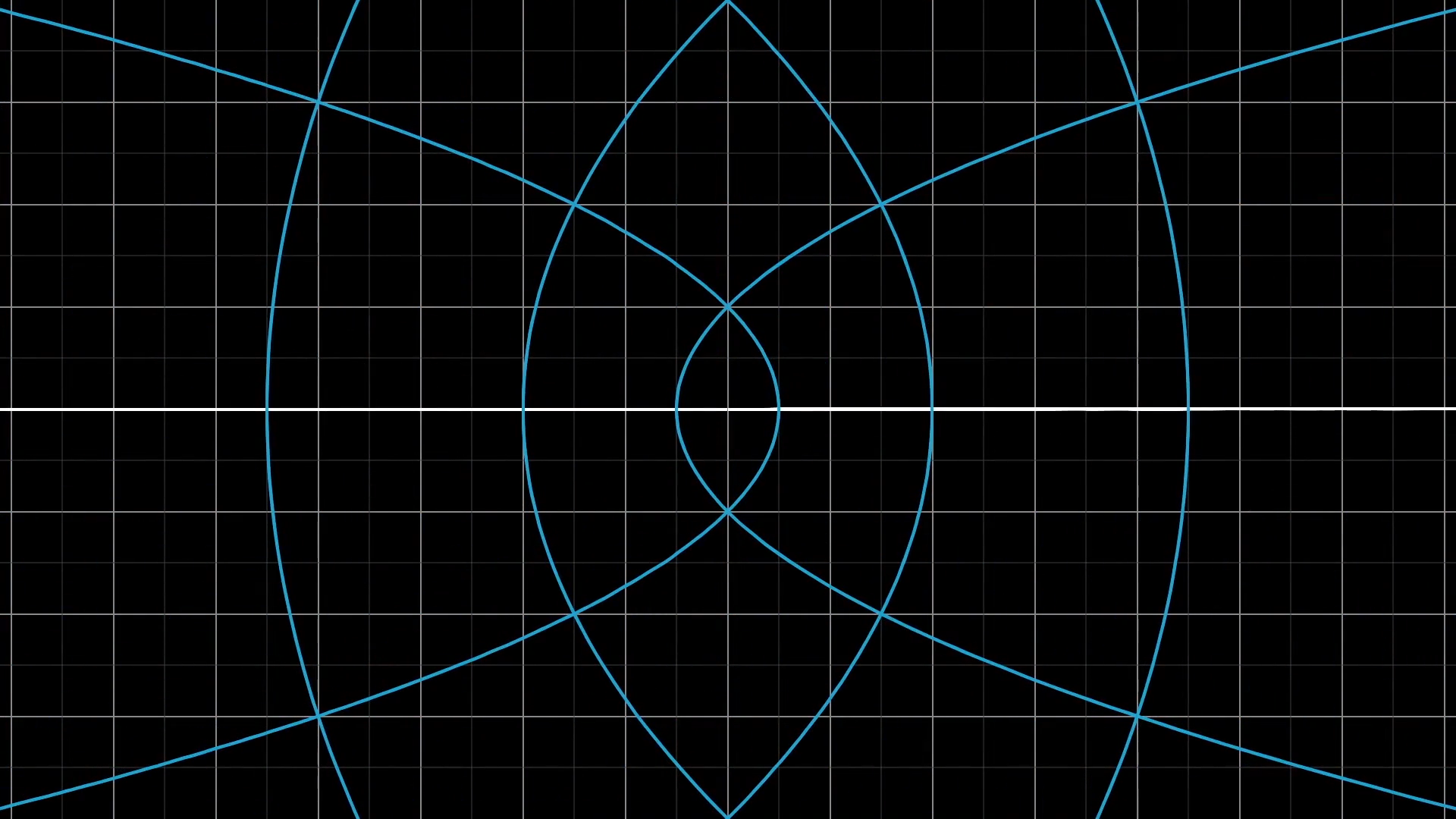
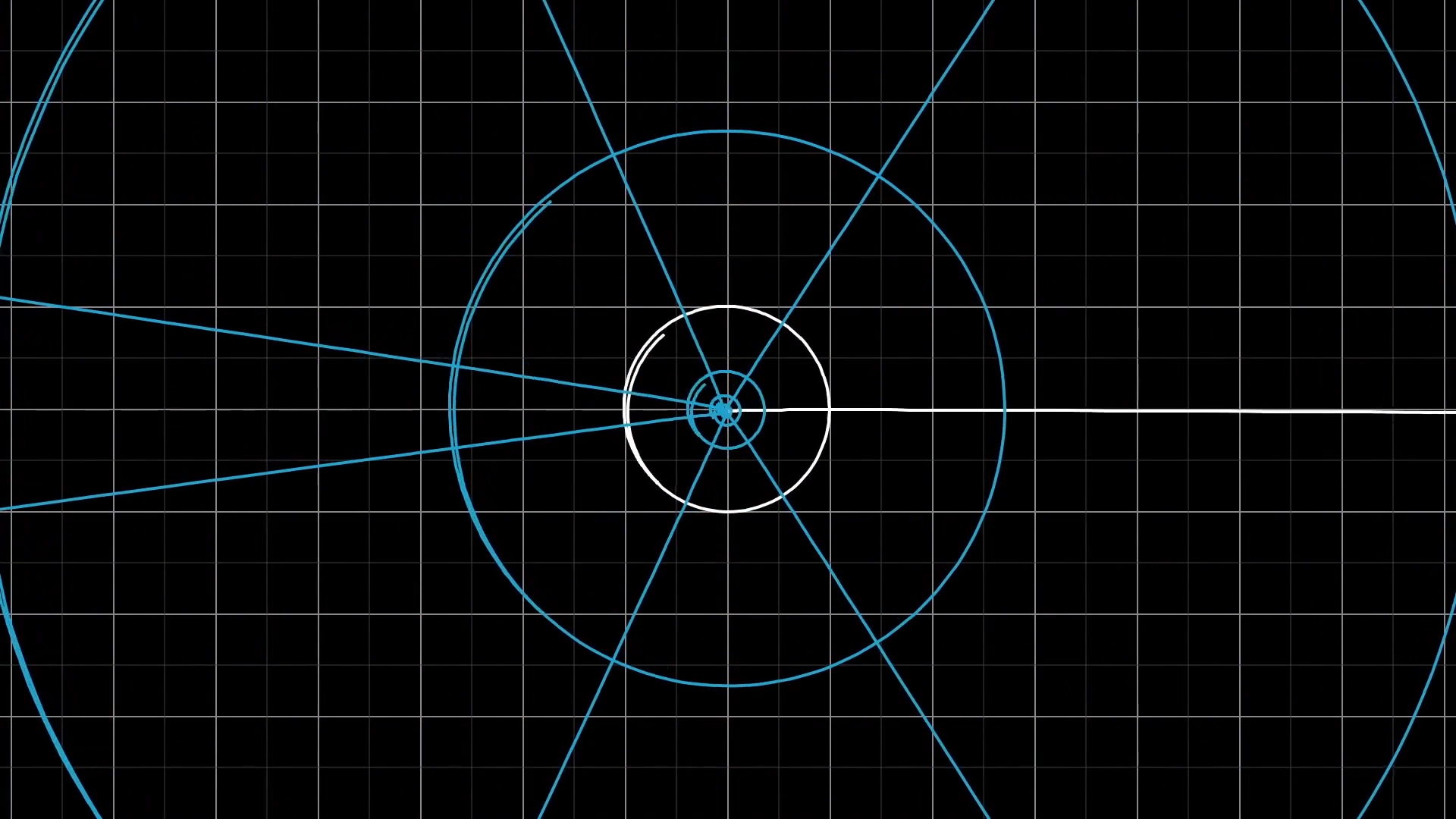
What makes a transformation "linear"?

As you can imagine, though, arbitrary transformations can look pretty complicated, but luckily linear algebra limits itself to a special type of transformation that's easier to understand called Linear transformations. Visually speaking, a transformation is "linear" if it has two properties: all lines must remain lines, without getting curved, and the origin must remain fixed in place.

For example, this right here would not be a linear transform, since the lines get all curvy.

And this one would not be a linear transformation because the origin moves.

This one here fixes the origin, and it might look like it keeps lines straight, but that's just because we're only showing horizontal and vertical grid lines.

When you see what it does to a diagonal line, it becomes clear that it's not a linear transformation at all, since it turns that line all curvy.

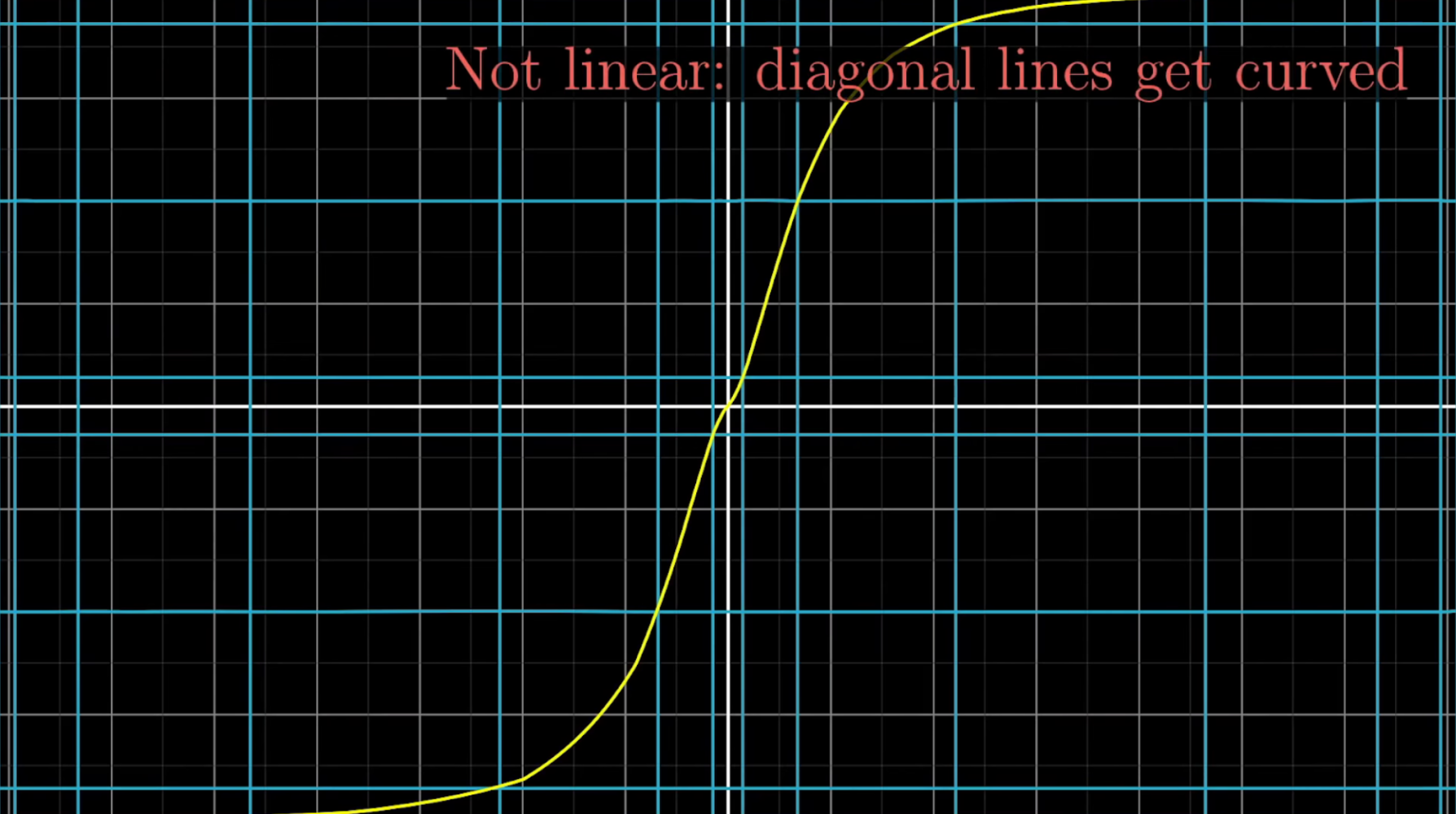
In general you should think of linear transformations as keeping grid lines parallel and evenly spaced, although they might change the angles between perpendicular grid lines. Some linear transformations are simple to think about, like rotations about the origin. Others are a little trickier to describe with words.

Some linear transformations are simple to think about, like rotations about the origin.

Others, as we will see later, are a little trickier to describe with words.

Which of the transformations in the image below are linear?

Matrices

How do you think you could do these transformations numerically? If you were, say, programming some animations to make a video teaching the topic, what formula do you give the computer so that if you give it the coordinates of a vector, it can tell you the coordinates of where that vector lands.

It turns out, you only need to record where the two basis vectors $\hat{\imath}$ and $\hat{\jmath}$ go, and everything else will follow.

StillAnimation

For example, consider the vector $\vec{\mathbf{v}}$ with coordinates $\begin{bmatrix}-1\\2\end{bmatrix}$, meaning it is equal to $-1\hat{\imath} + 2\hat{\jmath}$.

If we play some transformation, and follow where all three of these vectors go, the property that grid lines remain parallel and evenly spaced has a really important consequence: the place where $\vec{\mathbf{v}}$ lands will be $(-1)$ times the vector where $\hat{\imath}$ landed, plus $2$ times the vector where $\hat{\jmath}$ landed.

StillAnimation

In other words, it started off as a certain linear combination of $\hat{\imath}$ and $\hat{\jmath}$, and it ended up at that same linear combination of where those two vectors landed.

Now, given that we're actually showing you the full transformation, you could have just looked to see that $\vec{\mathbf{v}}$ has coordinates $\left[\begin{array}{c} 5 \\ 2 \end{array}\right]$, but the cool part here is that this gives us a technique to deduce where the vector lands without needing to watch the transformation.

This is a good point to pause and ponder, because it's pretty important.

So long as we have a record of where $\hat{\imath}$ and $\hat{\jmath}$ land, this technique works for any vector that is passed to the transformation function.

StillAnimation

Writing the vector with more general coordinates, $x$ and $y$: It will land on $x$ times the vector where $\hat{\imath}$ lands, $\left[\begin{array}{c} 1 \\ -2 \end{array}\right]$, plus $y$ time the vector where $\hat{\jmath}$ lands, $\left[\begin{array}{c} 3 \\ 0 \end{array}\right]$.

Carrying out that sum, we see that it lands on $\left[\begin{array}{c} 1 x+3 y \\ -2 x+0 y \end{array}\right]$. Given any vector you can tell where it lands using this formula.

What all of this is saying is that the two-dimensional linear transformation is completely described by just four numbers: The two coordinates for where $\hat{\imath}$ lands, and the two coordinates for where $\hat{\jmath}$ lands. Isn't that cool?

It's common to package these four numbers into a 2x2 grid of numbers, called a “2x2 matrix”, where you can interpret the columns as the two special vectors where $\hat{\imath}$ and $\hat{\jmath}$ land.

If you're given a 2x2 matrix describing a linear transformation, and a specific vector, and you want to know where the linear transformation takes that vector, you take the coordinates of that vector, multiply them by the corresponding column of the matrix, then add together what you get. This corresponds with the idea of adding scaled versions of our new basis vectors.

When you do this super generally, with a matrix that has entries $\left[\begin{array}{cc}a & b \\c & d\end{array}\right]$, and a vector $\left[\begin{array}{c} x \\ y \end{array}\right]$, what's the resulting vector? Remember here that the first column $\left[\begin{array}{c} a \\ c \end{array}\right]$ corresponds to the place where the first basis vector lands, and the second column $\left[\begin{array}{c} b \\ d \end{array}\right]$ is the place where the second basis vector lands.

Well, it will be $x \left[\begin{array}{c} a \\ c \end{array}\right] + y \left[\begin{array}{c} b \\ d \end{array}\right]$ and, putting this together, you get a vector $\left[\begin{array}{c} ax + by \\ cx + dy \end{array}\right]$.

You could even define this as "matrix vector multiplication" when you put the matrix to the left of the vector like a function. Then you could make high schoolers memorize this formula for no apparent reason.

But isn't it more fun to think about the columns as the transformed versions of your basis vectors, and to think of the result as the appropriate linear combination of those vectors?

Examples

Let's practice describing a few linear transformations with matrices.

Rotation

For example, if we rotate all of space $90$ degrees counterclockwise, then $\hat{\imath}$ lands at the coordinates $\left[\begin{array}{c} 0 \\ 1 \end{array}\right]$, and $\hat{\jmath}$ lands at the coordinates $\left[\begin{array}{c} -1 \\ 0 \end{array}\right]$, so the matrix we end up with has columns $\left[\begin{array}{c} 0 \\ 1 \end{array}\right]$ and $\left[\begin{array}{c} -1 \\ 0 \end{array}\right]$.

StillAnimation

To figure out what happens to any vector after a $90$ degree counterclockwise rotation, you can multiply its coordinates by this matrix.

Shear

Here's a fun transformation with a special name, called a “shear”.

StillAnimation

In it, $\hat{\imath}$ remains fixed, so the first column of the matrix is $\left[\begin{array}{c} 1 \\ 0 \end{array}\right]$, but $\hat{\jmath}$ moves over to the coordinates $\left[\begin{array}{c} 1 \\ 1 \end{array}\right]$, which becomes the second column of the matrix.

And at the risk of being redundant, figuring out how a shear transforms a given vector comes down to multiplying this matrix by that vector.

Transformation from a Matrix

What about the other way around? If we are given a matrix, say with columns $\left[\begin{array}{c} 1 \\ 2 \end{array}\right]$ and $\left[\begin{array}{c} 3 \\ 1 \end{array}\right]$, can you deduce what it's transformation looks like? Pause and take a moment to see if you can imagine it.

Your answer:

?Submit

Our answer:

One way to imagine it is to first move $\hat{\imath}$ to $\left[\begin{array}{c} 1 \\ 2 \end{array}\right]$, then move $\hat{\jmath}$ to $\left[\begin{array}{c} 3 \\ 1 \end{array}\right]$, always moving the rest of space in such a way that keeps the grid lines parallel and evenly spaced.

StillAnimation

Linearly Dependent Columns

If the vectors that $\hat{\imath}$ and $\hat{\jmath}$ land on are linearly dependent, which if you recall from the last chapter means one is a scaled version of the other, it means the linear transformation squishes all of 2d space onto the line where those vectors sit, also known as the one-dimensional span of these two linearly dependent vectors.

StillAnimation

Formal Properties

There's an unimaginably large number of possible transformations, many which are rather complicated to think about. As we discussed, linear algebra limits itself to a special type of transformation called a linear transformation which we defined as a transformation where grid lines remain parallel and evenly spaced. In addition to the geometric notion of "linearity" we can also express that a function is linear if it satisfies the following two properties:

To help appreciate just how constraining these two properties are, and to reason about what this implies a linear transformation must look like, consider the important fact from the last chapter that when you write down a vector with coordinates, say $\vec{\mathbf{v}} = \begin{bmatrix}-1\\2\end{bmatrix}$, you are effectively writing it as a linear combination of two basis vectors.

If you consider how the transformation acts separately on the two vectors that make up the linear combination, respectively $-1\hat{\imath}$ and ${2\hat{\jmath}}$, then the consequence of the transformation preserving sums is that $L(\vec{\mathbf{v}}) = L(-1 \hat{\imath})+L(2 \hat{\jmath})$.

StillAnimation

Since the transformation preserves scaling, we can rewrite the linear combination as the transformed basis vectors multiplied by the coordinates of the input vector.

This is why if you know where the two basis vectors $\hat{\imath}$ and $\hat{\jmath}$ go, everything else follows. For that matter, if you have any other pair of vectors spanning 2d space, knowing where they land will determine where everything else goes, but because $\hat{\imath}$ and $\hat{\jmath}$ are the standard choice for a basis we write matrices in terms of them.

Why do we know the origin must remain fixed in place using these formal properties?

Conclusion

Understanding how matrices can be thought of as transformation is a powerful mental tool for understanding the various constructs and definitions concerning matrices, which we'll explore as the series continues. This includes the ideas of matrix multiplication, determinants, how to solve systems of equations, what eigenvalues are, and much more. In all these cases, holding the picture of a linear transformation in your head can make the computations much more understandable.

On the flip side, there are cases where you may want to actually describe manipulations of space; again graphics programmings offers a wealth of examples. In those cases, knowing that matrices give a way to describe these transformations symbolically, in a manner conducive to concrete computations, is exceedingly helpful.